
分析 (1)化函數f(x)為正弦型函數,根據f(x)的最小正周期是π求出ω,寫出f(x)解析式;
根據正弦函數的單調性求出f(x)在x∈(0,π)上的單調遞增區間;
(2)根據x∈[$\frac{π}{8}$,$\frac{3π}{8}$]時2x-$\frac{π}{6}$的取值范圍,再求出對應函數f(x)的最值即可.
解答 解:(1)函數f(x)=4cosωxsin(ωx-$\frac{π}{6}$)
=4cosωx($\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx)
=2$\sqrt{3}$sinωxcosωx-2cos2ωx+1-1
=$\sqrt{3}$sin2ωx-cos2ωx-1
=2sin(2ωx-$\frac{π}{6}$)-1,
且f(x)的最小正周期是$\frac{2π}{2ω}=π$,所以ω=1;
從而f(x)=2sin(2x-$\frac{π}{6}$)-1;
令$-\frac{π}{2}+2kπ≤2x-\frac{π}{6}≤\frac{π}{2}+2kπ$,
解得$-\frac{π}{6}+kπ≤x≤\frac{π}{3}+kπ({k∈Z})$,
所以函數f(x)在x∈(0,π)上的單調遞增區間為$({0,\frac{π}{3}}]$和$({\frac{5π}{6},π})$.
(2)當x∈[$\frac{π}{8}$,$\frac{3π}{8}$]時,2x∈[$\frac{π}{4}$,$\frac{3π}{4}$],
所以2x-$\frac{π}{6}$∈[$\frac{π}{12}$,$\frac{7π}{12}$],
所以2sin(2x-$\frac{π}{6}$)∈[$\frac{\sqrt{6}-\sqrt{2}}{2}$,2],
所以當2x-$\frac{π}{6}$=$\frac{π}{12}$,即x=$\frac{π}{8}$時f(x)取得最小值$\frac{\sqrt{6}-\sqrt{2}}{2}$-1,
當2x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{3}$時f(x)取得最大值1;
所以f(x)在$[{\frac{π}{8},\frac{3π}{8}}]$上的最大值和最小值分別為$1、\frac{{\sqrt{6}-\sqrt{2}}}{2}-1$.
點評 本題考查了三角函數的化簡以及三角函數的圖象與性質的應用問題,是基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{2}{5{e}^{2}}$,$\frac{1}{3e}$) | B. | [$\frac{1}{3e}$,$\frac{\sqrt{e}}{4e}$) | C. | [$\frac{1}{3e}$,e] | D. | [$\frac{\sqrt{e}}{4e}$,e] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(\frac{ln4}{3},+∞)$ | B. | $(\frac{ln2}{3},+∞)$ | C. | $(\frac{{\sqrt{3}}}{2},+∞)$ | D. | $(\frac{{\sqrt{e}}}{3},+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(1,\frac{{\sqrt{6}}}{2}]$ | B. | $[\frac{{\sqrt{6}}}{2},+∞)$ | C. | $(1,\frac{{\sqrt{6}}}{2})$ | D. | $(\frac{{\sqrt{6}}}{2},+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
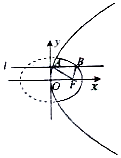 如圖動直線l:y=b與拋物線y2=4x交于點A,與橢圓$\frac{x^2}{2}+{y^2}$=1交于拋物線右側的點B,F為拋物線的焦點,則|AF|+|BF|+|AB|的最大值為( )
如圖動直線l:y=b與拋物線y2=4x交于點A,與橢圓$\frac{x^2}{2}+{y^2}$=1交于拋物線右側的點B,F為拋物線的焦點,則|AF|+|BF|+|AB|的最大值為( )| A. | $3\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2)∪(-2,2) | D. | (0,2)∪(2,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com