
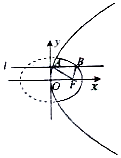
 如圖動直線l:y=b與拋物線y2=4x交于點A,與橢圓$\frac{x^2}{2}+{y^2}$=1交于拋物線右側的點B,F為拋物線的焦點,則|AF|+|BF|+|AB|的最大值為( )
如圖動直線l:y=b與拋物線y2=4x交于點A,與橢圓$\frac{x^2}{2}+{y^2}$=1交于拋物線右側的點B,F為拋物線的焦點,則|AF|+|BF|+|AB|的最大值為( )| A. | $3\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
分析 利用拋物線的定義,求出拋物線的焦點坐標,求出B的坐標,轉化所求的距離為x的函數的關系式,然后求解最大值即可.
解答  解:直線l:y=b與拋物線y2=4x交于點A,F為拋物線的焦點,直線y=b與x=-1的交點為D,由拋物線定義,可知AF=AD,|AF|+|BF|+|AB|的最大值,
解:直線l:y=b與拋物線y2=4x交于點A,F為拋物線的焦點,直線y=b與x=-1的交點為D,由拋物線定義,可知AF=AD,|AF|+|BF|+|AB|的最大值,
就是BD+BF的最大值,F(1,0),設B(x,b),橢圓$\frac{x^2}{2}+{y^2}$=1的焦點坐標(1,0).
可得$\frac{{x}^{2}}{2}+{b}^{2}=1$,|AF|+|BF|+|AB|=x+1+$\sqrt{(x-1)^{2}+{b}^{2}}$=x+1+$\sqrt{(x-1)^{2}+1-\frac{{x}^{2}}{2}}$
=x+1+$\sqrt{\frac{{x}^{2}}{2}-2x+2}$=x+1+$\frac{\sqrt{2}}{2}(2-x)$=1+$\sqrt{2}$+x(1-$\frac{\sqrt{2}}{2}$),x∈(0,$\sqrt{2}$].
當x=$\sqrt{2}$時,1+$\sqrt{2}$+x(1-$\frac{\sqrt{2}}{2}$)=1+$\sqrt{2}$+$\sqrt{2}$(1-$\frac{\sqrt{2}}{2}$)=2$\sqrt{2}$,
故選:D.
點評 本題考查直線與橢圓以及拋物線的位置關系的綜合應用,考查函數思想的應用,是中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{9}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0°≤α<180° | B. | 45°≤α<180° | ||
| C. | 0°≤α≤45°或90°<α<180° | D. | 0°≤α≤45°或90°≤α<180° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com