
分析 推導出an=1+(n-1)×2=2n-1,不等式$\frac{λ}{{{a_{n+1}}}}≤\frac{n+8}{n}$對任意n∈N*恒成立,等價于$\frac{λ}{2(n+1)-1}$$≤\frac{n+8}{n}$對任意n∈N*恒成立,由此利用均值定理能求出實數λ的最大值.
解答 解:∵數列{an}是各項均不為零的等差數列,Sn為其前n項和,且${a_n}=\sqrt{{S_{2n-1}}}({n∈{N^*}})$.
∴${{a}_{n}}^{2}={S}_{2n-1}$,
∴${{a}_{1}}^{2}={S}_{1}={a}_{1}$,由a1>0,解得a1=1,
${{a}_{2}}^{2}={S}_{3}={a}_{1}+{a}_{2}+{a}_{3}$=3a2,由a2>0,解得a2=3,
∴公差d=a2-a1=2,
an=1+(n-1)×2=2n-1.
∵不等式$\frac{λ}{{{a_{n+1}}}}≤\frac{n+8}{n}$對任意n∈N*恒成立,
∴$\frac{λ}{2(n+1)-1}$$≤\frac{n+8}{n}$對任意n∈N*恒成立,
∴$λ≤\frac{n+8}{n}×(2n+1)$=$\frac{2{n}^{2}+17n+8}{n}$=$2n+\frac{8}{n}+17$≥2$\sqrt{2n×\frac{8}{n}}$+17=25.
當且僅當2n=$\frac{8}{n}$,即n=2時,取等號,
∴實數λ的最大值為25.
故答案為:25.
點評 本題考查實數的最大值的求法,是中檔題,解題時要認真審題,注意等差數列的性質和均值定理的合理運用.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
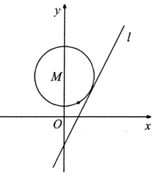 已知直線l:y=2x+n,n∈R,圓M的圓心在y軸,且過點(1,1).
已知直線l:y=2x+n,n∈R,圓M的圓心在y軸,且過點(1,1).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [2,3] | B. | [-1,2] | C. | [-1,0] | D. | [-1,0]∪[2,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,2] | B. | [0,1] | C. | [-1,3) | D. | [-1,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2({\sqrt{3}+1})$ | B. | $2({\sqrt{3}-1})$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{\sqrt{3}}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com