
分析 (Ⅰ)(i)求出函數的導數,通過討論b的范圍,求出函數的單調區間,從而求出函數的極值點,
(ii)得到函數g(x)有且僅有一個零點x=1,即方程2${{x}_{0}}^{3}$+x0-3=0的根為x0=1,從而求出b的值即可;
(Ⅱ)假設存在,根據題意得到${{x}_{1}}^{3}$+a${{x}_{1}}^{2}$+(b-1)x1+3=0.①,3${{x}_{1}}^{2}$+2ax1+b=0.②,得到a2-3b=-$\frac{9}{2}$,這與a2-3b>0相矛盾!判斷結論即可.
解答 解:(Ⅰ)f(x)的定義域為R,且f′(x)=3x2+2ax+b.[(1分)]
當a=0時,f′(x)=3x2+b;
(ⅰ)①當b≥0時,顯然f(x)在R上單調遞增,無極值點.[(2分)]
②當b<0時,令f′(x)=0,解得:x=±$\sqrt{-\frac{b}{3}}$.[(3分)]
f(x)和f′(x)的變化情況如下表:
| x | (-∞,-$\sqrt{-\frac{b}{3}}$) | -$\sqrt{-\frac{b}{3}}$ | (-$\sqrt{-\frac{b}{3}}$,$\sqrt{-\frac{b}{3}}$) | $\sqrt{-\frac{b}{3}}$ | ($\sqrt{-\frac{b}{3}}$,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↘ | ↗ |
點評 本題考查了函數的單調性、極值問題,考查導數的應用以及新定義問題,分類討論思想,是一道綜合題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
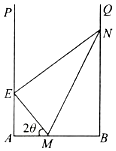 某地擬在一個U形水面PABQ(∠A=∠B=90°)上修一條堤壩(E在AP上,N在BQ上),圍出一個封閉區域EABN,用以種植水生植物.為了美觀起見,決定從AB上點M處分別向點E,N拉2條分割線ME,MN,將所圍區域分成3個部分(如圖),每部分種植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,設所拉分割線總長度為l.
某地擬在一個U形水面PABQ(∠A=∠B=90°)上修一條堤壩(E在AP上,N在BQ上),圍出一個封閉區域EABN,用以種植水生植物.為了美觀起見,決定從AB上點M處分別向點E,N拉2條分割線ME,MN,將所圍區域分成3個部分(如圖),每部分種植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,設所拉分割線總長度為l.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com