
分析 (Ⅰ)由函數的對稱中心可得2×$\frac{π}{8}$+φ=kπ,k∈Z,結合φ的范圍即可求得φ值;
(Ⅱ)直接利用復合函數的單調性求函數y=f(x)的單調遞增區間.
解答 解:(Ⅰ)由函數f(x)=sin(2x+φ)+1(-π<φ<0)圖象的一個對稱中心坐標為$(\frac{π}{8},1)$,
得2×$\frac{π}{8}$+φ=kπ,k∈Z,∴φ=-$\frac{π}{4}$+kπ,k∈Z,
又∵-π<φ<0,∴k=0時,得φ=-$\frac{π}{4}$;
(Ⅱ)f(x)=sin(2x-$\frac{π}{4}$)+1,
由$-\frac{π}{2}$+2kπ≤2x-$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
得-$\frac{π}{8}$+kπ≤x≤$\frac{3π}{8}$+kπ,k∈Z,
即函數f(x)的單調遞增區間為[$-\frac{π}{8}$+kπ,$\frac{3π}{8}$+kπ],k∈Z.
點評 本題考查y=Asin(ωx+φ)型函數的圖象和性質,著重考查三角函數的對稱性,是基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | $\overrightarrow{a}$,$\overrightarrow{b}$是共線向量且方向相反 | ||
| C. | $\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{a}$與$\overrightarrow{b}$方向相同 | D. | $\overrightarrow{a}$,$\overrightarrow{b}$無論什么關系均可 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,正方形ADMN與矩形ABCD所在平面互相垂直 AB=6,AD=3
如圖,正方形ADMN與矩形ABCD所在平面互相垂直 AB=6,AD=3查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
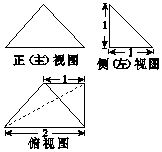
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{5}$ | B. | $\frac{2π}{5}$ | C. | $\frac{4π}{5}$ | D. | $\frac{6π}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com