
【題目】如圖,已知橢圓C:![]() 的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為
的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為![]() ,|F1F2|=
,|F1F2|=![]() ,O為坐標原點.
,O為坐標原點.
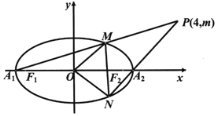
(1)求橢圓C的方程;
(2)設過點P(4,m)的直線PA1,PA2與橢圓分別交于點M,N,其中m>0,求![]() 的面積S的最大值.
的面積S的最大值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由離心率為![]() ,|F1F2|=2
,|F1F2|=2![]() ,列式計算a,b,即可得橢圓C的方程.
,列式計算a,b,即可得橢圓C的方程.
(2)將直線PA1,PA1的方程:y![]() ,y
,y![]() 分別與橢圓方程聯立,得到M、N的坐標,可得直線MN過定點(1,0),故設MN的方程為:x=ty+1,由
分別與橢圓方程聯立,得到M、N的坐標,可得直線MN過定點(1,0),故設MN的方程為:x=ty+1,由![]() 結合韋達定理,可得△OMN的面積S
結合韋達定理,可得△OMN的面積S![]() 2
2![]() ,再利用函數單調性即可求出面積最大值.
,再利用函數單調性即可求出面積最大值.
(1)∵離心率為![]() ,
,![]() ,
,
∴ ,∴
,∴![]() ,
,![]() ,則b=1
,則b=1
∴橢圓C的方程的方程為:![]()
(2)由(1)得A1(-2,0),A2(2,0),
直線PA1,PA1的方程分別為:![]() ,
,![]()
由 ,得
,得![]()
∴![]() ,可得
,可得![]() ,
,![]()
由 ,可得
,可得![]()
∴![]() ,可得
,可得![]() ,
,![]()
![]() ,
,
直線MN的方程為:![]() ,
,
![]()
![]()
![]()
可得直線MN過定點(1,0),故設MN的方程為:![]()
由 得
得![]()
設![]() ,
,![]() ,則
,則![]() ,
,![]()
∴![]() ,
,
∴![]() 的面積
的面積![]()
令![]() ,則
,則![]()
∵![]() ,且函數
,且函數![]() 在
在![]() 遞增,
遞增,
∴當![]() ,S取得最大值
,S取得最大值![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數y= 4cos2x+4![]() sinxcosx-2,(x∈R)
sinxcosx-2,(x∈R)
(1)求函數的最小正周期;
(2)求函數的最大值及其相對應的x值;
(3)寫出函數的單調增區間;
(4)寫出函數的對稱軸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC-A1B1C1中,底面ABC為等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
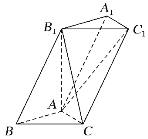
(I) 證明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1與平面BCB1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年初,新冠肺炎疫情襲擊全國,對人民生命安全和生產生活造成嚴重影響.在黨和政府強有力的抗疫領導下,我國控制住疫情后,一方面防止境外疫情輸入,另一方面逐步復工復產,減輕經濟下降對企業和民眾帶來的損失.為降低疫情影響,某廠家擬在2020年舉行某產品的促銷活動,經調查測算,該產品的年銷售量(即該廠的年產量)![]() 萬件與年促銷費用
萬件與年促銷費用![]() 萬元(
萬元(![]() )滿足
)滿足![]() (
(![]() 為常數),如果不搞促銷活動,則該產品的年銷售量只能是2萬件.已知生產該產品的固定投入為8萬元,每生產一萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍(此處每件產品年平均成本按
為常數),如果不搞促銷活動,則該產品的年銷售量只能是2萬件.已知生產該產品的固定投入為8萬元,每生產一萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍(此處每件產品年平均成本按![]() 元來計算)
元來計算)
(1)將2020年該產品的利潤![]() 萬元表示為年促銷費用
萬元表示為年促銷費用![]() 萬元的函數;
萬元的函數;
(2)該廠家2020年的促銷費用投入多少萬元時,廠家的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國第一高摩天輪“南昌之星摩天輪”高度為![]() ,其中心
,其中心![]() 距地面
距地面![]() ,半徑為
,半徑為![]() ,若某人從最低點
,若某人從最低點![]() 處登上摩天輪,摩天輪勻速旋轉,那么此人與地面的距離將隨時間
處登上摩天輪,摩天輪勻速旋轉,那么此人與地面的距離將隨時間![]() 變化,
變化,![]() 后達到最高點,從登上摩天輪時開始計時.
后達到最高點,從登上摩天輪時開始計時.
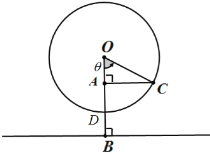
(1)求出人與地面距離![]() 與時間
與時間![]() 的函數解析式;
的函數解析式;
(2)從登上摩天輪到旋轉一周過程中,有多長時間人與地面距離大于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知具有線性相關關系的兩個變量![]() 之間的幾組數據如下表所示:
之間的幾組數據如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并估計當
,并估計當![]() 時,
時, ![]() 的值;
的值;
(2)將表格中的數據看作五個點的坐標,則從這五個點中隨機抽取2個點,求恰有1個點落在直線![]() 右下方的概率.
右下方的概率.
參考公式: 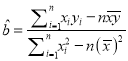 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4.
的兩個焦點與短軸的一個端點是等邊三角形的三個頂點,且長軸長為4.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 是橢圓
是橢圓![]() 的左頂點,經過左焦點
的左頂點,經過左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,求
兩點,求![]() 與
與![]() 的面積之差的絕對值的最大值.(
的面積之差的絕對值的最大值.(![]() 為坐標原點)
為坐標原點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓心在![]() 軸上的圓
軸上的圓![]() 經過兩點
經過兩點![]() 和
和![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)當![]() 時,
時,![]() 為直線
為直線![]() 上的定點,若圓
上的定點,若圓![]() 上存在唯一一點
上存在唯一一點![]() 滿足
滿足![]() ,求定點
,求定點![]() 的坐標;
的坐標;
(3)設點A,B為圓![]() 上任意兩個不同的點,若以AB為直徑的圓與直線
上任意兩個不同的點,若以AB為直徑的圓與直線![]() 都沒有公共點,求實數
都沒有公共點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com