
【題目】已知函數![]() (其中
(其中![]() ).
).
(1)討論![]() 的單調性;
的單調性;
(2)若對任意的![]() ,關于
,關于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)答案見解析;(2) ![]() .
.
【解析】試題分析:(1)先求函數導數,再討論二次方程根的個數與大小,確定導函數符號,進而確定函數單調性(2)先將不等式轉化為函數最值問題: ![]() ,再結合(1)討論函數最小值取法,最后根據不等式解集得
,再結合(1)討論函數最小值取法,最后根據不等式解集得![]() 的取值范圍.
的取值范圍.
試題解析:(1)![]() 的定義域為
的定義域為![]()
(i)若![]() ,則
,則![]() .由
.由![]() 得
得![]() 或
或![]() ;由
;由![]() 得
得![]()
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
(ii)若![]() ,則
,則![]() 在
在![]() 上單調遞增;
上單調遞增;
(iii)若![]() ,則
,則![]() ,由
,由![]() 得
得![]() 或
或![]() ;由
;由![]() 得
得![]()
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)由(1)知,(i)若![]() ,
,
當![]() 時,即
時,即![]() 時,
時, ![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
![]() ,故
,故![]() 對
對![]() 不恒成立;
不恒成立;
當![]() 時,即
時,即![]() 時,
時, ![]() 在
在![]() 上單調遞增,
上單調遞增, ![]()
![]()
(ii)若![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ,故
,故![]() ;
;
綜上所述, ![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】袋中有6個球,其中4個白球,2個紅球,從袋中任意取出兩球,求下列事件的概率:
(1) 取出的兩球1個是白球,另1個是紅球;
(2) 取出的兩球至少一個是白球。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,上頂點為
,上頂點為![]() ,若直線
,若直線![]() 的斜率為1,且與橢圓的另一個交點為
的斜率為1,且與橢圓的另一個交點為![]() ,
, ![]() 的周長為
的周長為![]() .
.
(1)求橢圓的標準方程;
(2)過點![]() 的直線
的直線![]() (直線
(直線![]() 的斜率不為1)與橢圓交于
的斜率不為1)與橢圓交于![]() 兩點,點
兩點,點![]() 在點
在點![]() 的上方,若
的上方,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() 的焦點為F,拋物線C與直線l1:
的焦點為F,拋物線C與直線l1:![]() 的一個交點為
的一個交點為![]() ,且
,且![]() (
(![]() 為坐標原點).
為坐標原點).
(Ⅰ)求拋物線C的方程;
(II)不過原點的直線l2與l1垂直,且與拋物線交于不同的兩點A,B,若線段AB的中點為P,且|OP|=|PB|,求△FAB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年
年![]() 月某城市國際馬拉松賽正式舉行,組委會對
月某城市國際馬拉松賽正式舉行,組委會對![]() 名裁判人員進(年齡均在
名裁判人員進(年齡均在![]() 歲到
歲到![]() 歲)行業務培訓,現按年齡(單位:歲)進行分組統計:第
歲)行業務培訓,現按年齡(單位:歲)進行分組統計:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如下:
,得到的頻率分布直方圖如下:
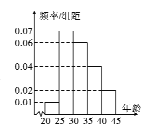
(1)若把這![]() 名裁判人員中年齡在
名裁判人員中年齡在![]() 稱為青年組,其中男裁判
稱為青年組,其中男裁判![]() 名;年齡在
名;年齡在![]() 的稱為中年組,其中男裁判
的稱為中年組,其中男裁判![]() 名.試完成
名.試完成![]() 列聯表并判斷能否在犯錯誤的概率不超過
列聯表并判斷能否在犯錯誤的概率不超過![]() 的前提下認為裁判員屬于不同的組別(青年組或中年組)與性別有關系?
的前提下認為裁判員屬于不同的組別(青年組或中年組)與性別有關系?
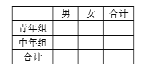
(2)培訓前組委會用分層抽樣調查方式在第![]() 組共抽取了
組共抽取了![]() 名裁判人員進行座談,若將其中抽取的第
名裁判人員進行座談,若將其中抽取的第![]() 組的人員記作
組的人員記作![]() ,第
,第![]() 組的人員記作
組的人員記作![]() ,第
,第![]() 組的人員記作
組的人員記作![]() ,若組委會決定從上述
,若組委會決定從上述![]() 名裁判人員中再隨機選
名裁判人員中再隨機選![]() 人參加新聞發布會,要求這
人參加新聞發布會,要求這![]() 組各選
組各選![]() 人,試求裁判人員
人,試求裁判人員![]() 不同時被選擇的概率;
不同時被選擇的概率;
附: 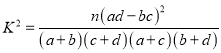
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的部分圖像如圖所示,將
的部分圖像如圖所示,將![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后得到函數
個單位長度后得到函數![]() 的圖象.
的圖象.

(1)求函數![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C滿足
中,角A,B,C滿足![]() ,且其外接圓的半徑R=2,求
,且其外接圓的半徑R=2,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為
的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為![]() ,|F1F2|=
,|F1F2|=![]() ,O為坐標原點.
,O為坐標原點.
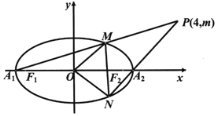
(1)求橢圓C的方程;
(2)設過點P(4,m)的直線PA1,PA2與橢圓分別交于點M,N,其中m>0,求![]() 的面積S的最大值.
的面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網約車的興起豐富了民眾出行的選擇,為民眾出行提供便利的同時也解決了很多勞動力的就業問題,據某著名網約車公司“滴滴打車”官網顯示,截止目前,該公司已經累計解決退伍軍人轉業為兼職或專職司機三百多萬人次,梁某即為此類網約車司機,據梁某自己統計某一天出車一次的總路程數可能的取值是20、22、24、26、28、![]() ,它們出現的概率依次是
,它們出現的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求這一天中梁某一次行駛路程X的分布列,并求X的均值和方差;
(2)網約車計費細則如下:起步價為5元,行駛路程不超過![]() 時,租車費為5元,若行駛路程超過
時,租車費為5元,若行駛路程超過![]() ,則按每超出
,則按每超出![]() (不足
(不足![]() 也按
也按![]() 計程)收費3元計費.依據以上條件,計算梁某一天中出車一次收入的均值和方差.
計程)收費3元計費.依據以上條件,計算梁某一天中出車一次收入的均值和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在海岸![]() 處,發現北偏東
處,發現北偏東![]() 方向,距離
方向,距離![]() 為
為![]() 海里的
海里的![]() 處有一艘走私船,在
處有一艘走私船,在![]() 處北偏西
處北偏西![]() 方向,距離
方向,距離![]() 為
為![]() 海里的
海里的![]() 處有一艘緝私艇奉命以
處有一艘緝私艇奉命以![]() 海里/時的速度追截走私船,此時,走私船正以
海里/時的速度追截走私船,此時,走私船正以![]() 海里/時的速度從
海里/時的速度從![]() 處向北偏東
處向北偏東![]() 方向逃竄.
方向逃竄.
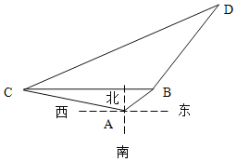
(1)問![]() 船與
船與![]() 船相距多少海里?
船相距多少海里?![]() 船在
船在![]() 船的什么方向?
船的什么方向?
(2)問緝私艇沿什么方向行駛才能最快追上走私船?并求出所需時間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com