
【題目】已知具有線性相關關系的兩個變量![]() 之間的幾組數據如下表所示:
之間的幾組數據如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并估計當
,并估計當![]() 時,
時, ![]() 的值;
的值;
(2)將表格中的數據看作五個點的坐標,則從這五個點中隨機抽取2個點,求恰有1個點落在直線![]() 右下方的概率.
右下方的概率.
參考公式: 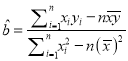 ,
, ![]() .
.
 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案科目:高中數學 來源: 題型:
【題目】如圖,MN分別是邊長為1的正方形ABCD的邊BCCD的中點,將正方形沿對角線AC折起,使點D不在平面ABC內,則在翻折過程中,有以下結論:

①異面直線AC與BD所成的角為定值.
②存在某個位置,使得直線AD與直線BC垂直.
③存在某個位置,使得直線MN與平面ABC所成的角為45°.
④三棱錐M-ACN體積的最大值為![]() .
.
以上所有正確結論的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年
年![]() 月某城市國際馬拉松賽正式舉行,組委會對
月某城市國際馬拉松賽正式舉行,組委會對![]() 名裁判人員進(年齡均在
名裁判人員進(年齡均在![]() 歲到
歲到![]() 歲)行業務培訓,現按年齡(單位:歲)進行分組統計:第
歲)行業務培訓,現按年齡(單位:歲)進行分組統計:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如下:
,得到的頻率分布直方圖如下:
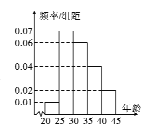
(1)若把這![]() 名裁判人員中年齡在
名裁判人員中年齡在![]() 稱為青年組,其中男裁判
稱為青年組,其中男裁判![]() 名;年齡在
名;年齡在![]() 的稱為中年組,其中男裁判
的稱為中年組,其中男裁判![]() 名.試完成
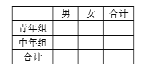
名.試完成![]() 列聯表并判斷能否在犯錯誤的概率不超過
列聯表并判斷能否在犯錯誤的概率不超過![]() 的前提下認為裁判員屬于不同的組別(青年組或中年組)與性別有關系?
的前提下認為裁判員屬于不同的組別(青年組或中年組)與性別有關系?
(2)培訓前組委會用分層抽樣調查方式在第![]() 組共抽取了
組共抽取了![]() 名裁判人員進行座談,若將其中抽取的第
名裁判人員進行座談,若將其中抽取的第![]() 組的人員記作
組的人員記作![]() ,第
,第![]() 組的人員記作
組的人員記作![]() ,第
,第![]() 組的人員記作
組的人員記作![]() ,若組委會決定從上述
,若組委會決定從上述![]() 名裁判人員中再隨機選
名裁判人員中再隨機選![]() 人參加新聞發布會,要求這
人參加新聞發布會,要求這![]() 組各選
組各選![]() 人,試求裁判人員
人,試求裁判人員![]() 不同時被選擇的概率;
不同時被選擇的概率;
附: 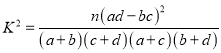
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為
的左、右項點分別為A1,A2,左右焦點分別為F1,F2,離心率為![]() ,|F1F2|=
,|F1F2|=![]() ,O為坐標原點.
,O為坐標原點.
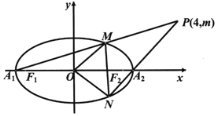
(1)求橢圓C的方程;
(2)設過點P(4,m)的直線PA1,PA2與橢圓分別交于點M,N,其中m>0,求![]() 的面積S的最大值.
的面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農場有一塊等腰直角三角形的空地![]() ,其中斜邊
,其中斜邊![]() 的長度為400米.為迎接“五一”觀光游,欲在邊界
的長度為400米.為迎接“五一”觀光游,欲在邊界![]() 上選擇一點
上選擇一點![]() ,修建觀賞小徑
,修建觀賞小徑![]() ,其中
,其中![]() 分別在邊界
分別在邊界![]() 上,小徑
上,小徑![]() 與邊界
與邊界![]() 的夾角都為
的夾角都為![]() .區域
.區域![]() 和區域
和區域![]() 內種植郁金香,區域
內種植郁金香,區域![]() 內種植月季花.
內種植月季花.

(1)探究:觀賞小徑![]() 與
與![]() 的長度之和是否為定值?請說明理由;
的長度之和是否為定值?請說明理由;
(2)為深度體驗觀賞,準備在月季花區域內修建小徑![]() ,當
,當![]() 點在何處時,三條小徑
點在何處時,三條小徑![]() 的長度和最小?
的長度和最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網約車的興起豐富了民眾出行的選擇,為民眾出行提供便利的同時也解決了很多勞動力的就業問題,據某著名網約車公司“滴滴打車”官網顯示,截止目前,該公司已經累計解決退伍軍人轉業為兼職或專職司機三百多萬人次,梁某即為此類網約車司機,據梁某自己統計某一天出車一次的總路程數可能的取值是20、22、24、26、28、![]() ,它們出現的概率依次是
,它們出現的概率依次是![]() 、
、![]() 、
、![]() 、
、![]() 、t、
、t、![]() .
.
(1)求這一天中梁某一次行駛路程X的分布列,并求X的均值和方差;
(2)網約車計費細則如下:起步價為5元,行駛路程不超過![]() 時,租車費為5元,若行駛路程超過
時,租車費為5元,若行駛路程超過![]() ,則按每超出
,則按每超出![]() (不足
(不足![]() 也按
也按![]() 計程)收費3元計費.依據以上條件,計算梁某一天中出車一次收入的均值和方差.
計程)收費3元計費.依據以上條件,計算梁某一天中出車一次收入的均值和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)經過點(
(a>b>0)經過點(![]() ,1),以原點為圓心、橢圓短半軸長為半徑的圓經過橢圓的焦點.
,1),以原點為圓心、橢圓短半軸長為半徑的圓經過橢圓的焦點.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設過點(-1,0)的直線l與橢圓C相交于A,B兩點,試問在x軸上是否存在一個定點M,使得![]() 恒為定值?若存在,求出該定值及點M的坐標;若不存在,請說明理由.
恒為定值?若存在,求出該定值及點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對函數f(x)=xsinx,現有下列命題:①函數f(x)是偶函數;②函數f(x)的最小正周期是2π;③點(π,0)是函數f(x)的圖象的一個對稱中心;④函數f(x)在區間![]() 上單調遞增,在區間
上單調遞增,在區間![]() 上單調遞減.其中是真命題的是________.(寫出所有真命題的序號)
上單調遞減.其中是真命題的是________.(寫出所有真命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com