
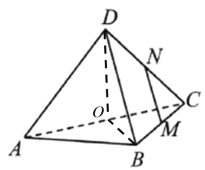
【題目】如圖,MN分別是邊長為1的正方形ABCD的邊BCCD的中點,將正方形沿對角線AC折起,使點D不在平面ABC內,則在翻折過程中,有以下結論:

①異面直線AC與BD所成的角為定值.
②存在某個位置,使得直線AD與直線BC垂直.
③存在某個位置,使得直線MN與平面ABC所成的角為45°.
④三棱錐M-ACN體積的最大值為![]() .
.
以上所有正確結論的序號是__________.
【答案】①③④
【解析】
設![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,得到
,得到![]() 平面
平面![]() ,從而可證①正確;假設
,從而可證①正確;假設![]() ,從而得到
,從而得到![]() 平面
平面![]() ,與已知矛盾,從而證明②錯誤,根據
,與已知矛盾,從而證明②錯誤,根據![]() ,得到
,得到![]() 與平面
與平面![]() 所成的角等于
所成的角等于![]() 與平面
與平面![]() 所成的角,即
所成的角,即![]() ,根據
,根據![]() 的范圍,從而證明③正確;
的范圍,從而證明③正確;![]() ,從而得到體積最大的情況,求出最大值,可得④正確.
,從而得到體積最大的情況,求出最大值,可得④正確.
設![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,
正方形![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,
,
即異面直線![]() 與
與![]() 所成的角為定值
所成的角為定值![]() .
.
故①正確.
若![]() ,而
,而![]() ,
,![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,
,
而![]() 中,
中,![]() ,
,
所以![]() 不可能為直角,故假設錯誤,
不可能為直角,故假設錯誤,
所以②錯誤.
因為![]()
![]() 分別是
分別是![]()
![]() 的中點,所以
的中點,所以![]() ,
,
所以![]() 與平面
與平面![]() 所成的角等于
所成的角等于![]() 與平面
與平面![]() 所成的角,
所成的角,
![]() 在平面
在平面![]() 的射影在
的射影在![]() 上,
上,
所以![]() 是
是![]() 與平面
與平面![]() 所成的角,
所成的角,
而![]() ,所以一定存在某個位置滿足
,所以一定存在某個位置滿足![]() ,
,
即存在某個位置,使得直線MN與平面所成的角為45°.
故③正確;
![]() ,底面
,底面![]() ,
,
所以當平面![]() 平面
平面![]() 時,
時,![]() 到平面
到平面![]() 的距離最大,
的距離最大,
此時三棱錐![]() 的體積最大,
的體積最大,
![]() ,
,
所以此時![]() ,
,
故④正確.
故答案為:①③④


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】已知過點A(0,1)且斜率為k的直線l與圓C:(x-2)2+(y-3)2=1交于M,N兩點.
(1)求k的取值范圍;
(2)若![]() =12,其中O為坐標原點,求|MN|.
=12,其中O為坐標原點,求|MN|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y= 4cos2x+4![]() sinxcosx-2,(x∈R)
sinxcosx-2,(x∈R)
(1)求函數的最小正周期;
(2)求函數的最大值及其相對應的x值;
(3)寫出函數的單調增區間;
(4)寫出函數的對稱軸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,曲線![]() 是以原點O為中心、
是以原點O為中心、![]() 為焦點的橢圓的一部分,曲線
為焦點的橢圓的一部分,曲線![]() 是以O為頂點、
是以O為頂點、![]() 為焦點的拋物線的一部分,A是曲線
為焦點的拋物線的一部分,A是曲線![]() 和
和![]() 的交點且
的交點且![]() 為鈍角,若
為鈍角,若![]() ,
,![]() .
.

(1)求曲線![]() 和
和![]() 的方程;
的方程;
(2)過![]() 作一條與
作一條與![]() 軸不垂直的直線,分別與曲線
軸不垂直的直線,分別與曲線![]() 依次交于B、C、D、E四點,若G為CD中點、H為BE中點,問
依次交于B、C、D、E四點,若G為CD中點、H為BE中點,問![]() 是否為定值?若是求出定值;若不是說明理由.
是否為定值?若是求出定值;若不是說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國有悠久的金石文化,印信是金石文化的代表之一.印信的形狀多為長方體、正方體或圓柱體,但南北朝時期的官員獨孤信的印信形狀是“半正多面體”(圖1).半正多面體是由兩種或兩種以上的正多邊形圍成的多面體.半正多面體體現了數學的對稱美.圖2是一個棱數為48的半正多面體,它的所有頂點都在同一個正方體的表面上,且此正方體的棱長為1.則該半正多面體共有________個面,其棱長為_________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC-A1B1C1中,底面ABC為等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
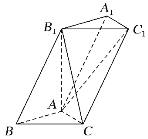
(I) 證明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1與平面BCB1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知具有線性相關關系的兩個變量![]() 之間的幾組數據如下表所示:
之間的幾組數據如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并估計當
,并估計當![]() 時,
時, ![]() 的值;
的值;
(2)將表格中的數據看作五個點的坐標,則從這五個點中隨機抽取2個點,求恰有1個點落在直線![]() 右下方的概率.
右下方的概率.
參考公式: 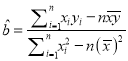 ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com