
【題目】已知函數 ![]() .
.
(1)求函數 ![]() 的單調區間和極值;
的單調區間和極值;
(2)是否存在實數 ![]() ,使得函數
,使得函數 ![]() 在
在 ![]() 上的最小值為
上的最小值為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】
(1)解:由題意知, ![]() .
.
由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所以函數
,所以函數 ![]() 的單調增區間是
的單調增區間是 ![]() ;
;
由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所以函數
,所以函數 ![]() 的單調減區間是
的單調減區間是 ![]() .
. ![]() 當
當 ![]() 時,函數
時,函數 ![]() 有極小值為
有極小值為 ![]()
(2)解:由(1)可知,當 ![]() 時,
時, ![]() 單調遞減,當
單調遞減,當 ![]() 時,
時, ![]() 單調遞增.
單調遞增.
①若 ![]() ,即
,即 ![]() 時,函數
時,函數 ![]() 在
在 ![]() 上為增函數,故函數
上為增函數,故函數 ![]() 的最小值為
的最小值為 ![]() ,顯然
,顯然 ![]() ,故不滿足條件.
,故不滿足條件.
②若 ![]() ,即
,即 ![]() 時,函數
時,函數 ![]() 在
在 ![]() 上為減函數,在
上為減函數,在 ![]() 上為增函數,故函數
上為增函數,故函數 ![]() 的最小值為
的最小值為 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,而
,而 ![]() ,故不滿足條件.
,故不滿足條件.
③若 ![]() ,即
,即 ![]() 時,函數
時,函數 ![]() 在在
在在 ![]() 上為減函數,故函數
上為減函數,故函數 ![]() 的最小值為
的最小值為 ![]() ,即
,即 ![]() ,而
,而 ![]() 不滿足條件,綜上所述,這樣的
不滿足條件,綜上所述,這樣的 ![]() 不存在
不存在
【解析】(1)根據題意求出原函數的導函數再利用導函數的正負得出原函數的增減性。(2)首先求出原函數的導函數由導函數大于零解出x的取值范圍然后對a分三種情況討論,再利用f ( x ) 在 [ 1 , e ] 上的最小值為 0求出a的值即可。
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減,以及對函數的極值與導數的理解,了解求函數
在這個區間單調遞減,以及對函數的極值與導數的理解,了解求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,且
,且![]() .
.
(1)當![]() 時,寫出
時,寫出![]() 的通項公式(直接寫出答案,無需過程);
的通項公式(直接寫出答案,無需過程);
(2)求最小整數![]() ,使得當
,使得當![]() 時,
時, ![]() 是單調遞增數列;
是單調遞增數列;
(3)是否存在![]() 使得
使得![]() 是等比數列?若存在請求出;若不存在請說明理由.
是等比數列?若存在請求出;若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,圓C的方程為ρ=2 ![]() sin
sin ![]() ,以極點為坐標原點,極軸為x軸的正半軸建立平面直角坐標系,直線l的參數方程為
,以極點為坐標原點,極軸為x軸的正半軸建立平面直角坐標系,直線l的參數方程為 ![]() (t為參數),判斷直線l和圓C的位置關系.
(t為參數),判斷直線l和圓C的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸標準煤)的幾組對照數據,
(噸標準煤)的幾組對照數據,

(1)求![]() ,
, ![]() ,
,
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)已知該廠技動前100噸甲產品的生產能耗為90噸標準煤.試根據(1)求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
已知![]() ,
, ![]() .
.
 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某種設備的使用年限![]() (年)與所支出的維修費用
(年)與所支出的維修費用![]() (萬元)有如下統計資料:
(萬元)有如下統計資料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
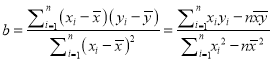 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 與
與![]() 具有線性相關關系,求出線性回歸方程;
具有線性相關關系,求出線性回歸方程;
(3)估計使用年限為10年時,維修費用約是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國數學家科拉茨1937年提出一個著名的猜想:任給一個正整數 ![]() ,如果
,如果 ![]() 是偶數,就將它減半(即
是偶數,就將它減半(即 ![]() );如果
);如果 ![]() 是奇數,則將它乘3加1(即
是奇數,則將它乘3加1(即 ![]() ),不斷重復這樣的運算,經過有限步后,一定可以得到1.對于科拉茨猜想,目前誰也不能證明。也不能否定,現在請你研究:如果對正整數
),不斷重復這樣的運算,經過有限步后,一定可以得到1.對于科拉茨猜想,目前誰也不能證明。也不能否定,現在請你研究:如果對正整數 ![]() (首項)按照上述規則旅行變換后的第9項為1(注:1可以多次出現),則
(首項)按照上述規則旅行變換后的第9項為1(注:1可以多次出現),則 ![]() 的所有不同值的個數為 .
的所有不同值的個數為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com