
【題目】條件 ![]() ;條件
;條件 ![]() :直線
:直線 ![]() 與圓
與圓 ![]() 相切,則
相切,則 ![]() 是
是 ![]() 的( )
的( )
A.充分必要條件
B.必要不充分條件
C.充分不必要條件
D.既不充分也不必要條件
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用 (基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費是與上一年度車輛發生道路交通安全違法行為或者道路交通事故的情況相聯系的.交強險第二年價格計算公式具體如下:交強險最終保費
元,在下一年續保時,實行的是費率浮動機制,保費是與上一年度車輛發生道路交通安全違法行為或者道路交通事故的情況相聯系的.交強險第二年價格計算公式具體如下:交強險最終保費![]() 基準保費
基準保費![]() (
(![]() 浮動比率
浮動比率![]() ).發生交通事故的次數越多,出險次數的就越多,費率也就越髙,具體浮動情況如下表:
).發生交通事故的次數越多,出險次數的就越多,費率也就越髙,具體浮動情況如下表:

某機構為了研究某一品牌普通6座以下私家車的投保情況,為此搜集并整理了100輛這一品牌普通6座以下私家車一年內的出險次數,得到下面的柱狀圖:

已知小明家里有一輛該品牌普通6座以下私家車且需要續保,續保費用為![]() 元.
元.
(1)記![]() 為事件“
為事件“![]() ”,求
”,求![]() 的估計值;
的估計值;
(2)求![]() 的平均估計值.
的平均估計值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]()
![]() 經過點
經過點 ![]() ,其離心率
,其離心率 ![]() .
.
(Ⅰ)求橢圓 ![]() 的方程;
的方程;
(Ⅱ)設動直線 ![]() 與橢圓
與橢圓 ![]() 相切,切點為
相切,切點為 ![]() ,且
,且 ![]() 與直線
與直線 ![]() 相交于點
相交于點 ![]() .
.
試問:在 ![]() 軸上是否存在一定點,使得以
軸上是否存在一定點,使得以 ![]() 為直徑的圓恒過該定點?若存在,
為直徑的圓恒過該定點?若存在,
求出該點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答題
(Ⅰ)已知函數f(x)=|x+1|+|x﹣a|(a>0),若不等式f(x)≥5的解集為{x|x≤﹣2或x≥3},求a的值;
(Ⅱ) 已知實數a,b,c∈R+ , 且a+b+c=m,求證: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的左、右焦點分別為
的左、右焦點分別為 ![]() 、
、 ![]() ,短軸兩個端點為
,短軸兩個端點為 ![]() 、
、 ![]() ,且四邊形
,且四邊形 ![]() 是邊長為2的正方形.
是邊長為2的正方形.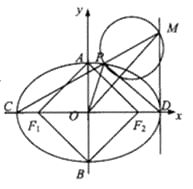
(1)求橢圓的方程;
(2)若 ![]() 、
、 ![]() 分別是橢圓長軸的左、右端點,動點
分別是橢圓長軸的左、右端點,動點 ![]() 滿足
滿足 ![]() ,連接
,連接 ![]() ,交橢圓于點
,交橢圓于點 ![]() .證明:
.證明: ![]() 為定值.
為定值.
(3)在(2)的條件下,試問 ![]() 軸上是否存異于點
軸上是否存異于點 ![]() 的定點
的定點 ![]() ,使得以
,使得以 ![]() 為直徑的圓恒過直線
為直徑的圓恒過直線 ![]() 、
、 ![]() 的交點,若存在,求出點
的交點,若存在,求出點 ![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知菱形 ABCD 中,對角線 AC 與 BD 相交于一點 O,∠A=60°,將△BDC 沿著 BD 折起得△BDC',連結 AC'.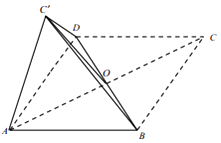
(Ⅰ)求證:平面 AOC'⊥平面 ABD;
(Ⅱ)若點 C'在平面 ABD 上的投影恰好是△ABD 的重心,求直線 CD 與底面 ADC'所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com