
【題目】國慶節來臨,某公園為了豐富廣大人民群眾的業余生活,特地以“我們都是中國人”為主題舉行猜謎語競賽.現有兩類謎語:一類叫事物謎,就是我們常說的謎語;另一類叫文義謎,也就是我們常說的燈謎,共8道題,其中事物謎4道題,文義謎4道題,孫同學從中任取3道題解答.
(1)求孫同學至少取到2道文義謎題的概率;
(2)如果孫同學答對每道事物謎題的概率都是![]() ,答對每道文義謎題的概率都是
,答對每道文義謎題的概率都是![]() ,且各題答對與否相互獨立,已知孫同學恰好選中2道事物謎題,1道文義謎題,用
,且各題答對與否相互獨立,已知孫同學恰好選中2道事物謎題,1道文義謎題,用![]() 表示孫同學答對題的個數,求隨機變量
表示孫同學答對題的個數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】(1)![]() ;(2)答案見解析,
;(2)答案見解析,![]() .
.
【解析】
(1)由題意可知孫同學至少取到2道文義謎題的有兩種情況:一是孫同學取到2道文義謎題,另一種是孫同學取到3道文義謎題,這兩種情況是互斥的,根據互斥事件概率的求法求解即可;
(2)由于孫同學從中任取3道題解答,用![]() 表示孫同學答對題的個數,所以
表示孫同學答對題的個數,所以![]() 可能的取值有0,1,2,3四種情況,分別求四種情況下的概率,即可得到分布列,進而可求出期望.
可能的取值有0,1,2,3四種情況,分別求四種情況下的概率,即可得到分布列,進而可求出期望.
解:(1)設“孫同學至少取到2道文義謎題”為事件![]() .
.
孫同學取到2道文義謎題共有![]() 種取法;
種取法;
孫同學取到3道文義謎題共有![]() 種取法,
種取法,
故![]() .
.
(2)易知![]() 的所有可能取值為0,1,2,3.
的所有可能取值為0,1,2,3.
則![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故隨機變量![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故隨機變量![]() 的數學期望
的數學期望![]() .
.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】下列說法中正確的是( )
A.若兩個隨機變量的線性相關性越強,則相關系數![]() 的值越接近于1
的值越接近于1
B.若正態分布![]() ,則
,則![]()
C.把某中學的高三年級560名學生編號:1到560,再從編號為1到10的10名學生中隨機抽取1名學生,其編號為![]() ,然后抽取編號為
,然后抽取編號為![]() ,
,![]() ,
,![]() ,…的學生,這樣的抽樣方法是分層抽樣
,…的學生,這樣的抽樣方法是分層抽樣
D.若一組數據0,![]() ,3,4的平均數是2,則該組數據的方差是
,3,4的平均數是2,則該組數據的方差是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]()
![]() .經過點
.經過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(其中點
兩點(其中點![]() 在
在![]() 軸上方),
軸上方),![]() 的周長為
的周長為![]() .
.
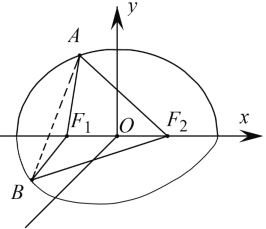
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖,把平面![]() 沿
沿![]() 軸折起來,使
軸折起來,使![]() 軸正半軸和
軸正半軸和![]() 軸確定的半平面,與
軸確定的半平面,與![]() 軸負半軸和
軸負半軸和![]() 軸所確定的半平面互相垂直,若折疊后
軸所確定的半平面互相垂直,若折疊后![]() 的周長為
的周長為![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,點E在AB上,AE=2EB=2,且DE⊥AB.以DE為折痕把△ADE折起,使點A到達點F的位置,且∠FEB=60°.
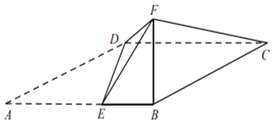
(1)求證:平面BFC⊥平面BCDE;
(2)若直線DF與平面BCDE所成角的正切值為![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() 側面
側面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,點
,點![]() 是棱
是棱![]() 的中點.
的中點.
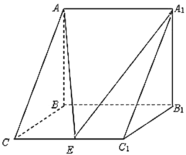
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,過曲線![]() 外的一點
外的一點![]() (其中
(其中![]() ,
,![]() 為銳角)作平行于
為銳角)作平行于![]() 的直線
的直線![]() 與曲線分別交于
與曲線分別交于![]() .
.
(Ⅰ) 寫出曲線![]() 和直線
和直線![]() 的普通方程(以極點為原點,極軸為
的普通方程(以極點為原點,極軸為![]() 軸的正半軸建系);
軸的正半軸建系);
(Ⅱ)若![]() 成等比數列,求
成等比數列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com