
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.
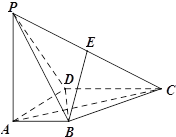
(1)證明:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 為棱
為棱![]() 上一點,滿足
上一點,滿足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)可以建立空間直角坐標系,利用向量數量積來證明![]() ,;(2)向量法:先求平面
,;(2)向量法:先求平面![]() 的法向量
的法向量![]() ,然后利用公式
,然后利用公式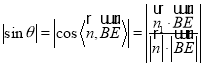 求直線
求直線![]() 與平面
與平面![]() 所成角的正弦值;(3)向量法:先求平面
所成角的正弦值;(3)向量法:先求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,再利用公式
,再利用公式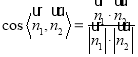 來求二面角
來求二面角![]() 的余弦值.
的余弦值.
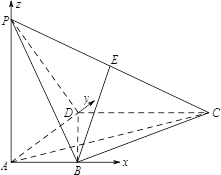
依題意,以點![]() 為原點建立空間直角坐標系(如圖),可得
為原點建立空間直角坐標系(如圖),可得![]() ,
,![]() ,由點
,由點![]() 為棱
為棱![]() 的中點,得
的中點,得![]() .
.
(1)向量![]() ,
,![]() ,故
,故![]() . ∴
. ∴![]() .
.
(2)向量![]() ,設
,設![]() 為平面
為平面![]() 的法向量,則
的法向量,則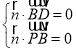 ,即
,即![]() ,
,
不妨令![]() ,可得
,可得![]() 為平面
為平面![]() 的一個法向量.
的一個法向量.
于是有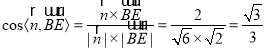 ,
,
∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
(3)![]() ,
,
由點![]() 在棱
在棱![]() 上,故
上,故![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,即
,即![]() .
.
設![]() 為平面
為平面![]() 的法向量,則
的法向量,則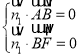 ,即
,即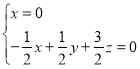 ,不妨令
,不妨令![]() ,可得
,可得![]() 為平面
為平面![]() 的一個法向量.取平面
的一個法向量.取平面![]() 的法向量
的法向量![]() ,則
,則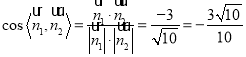 .
.
易知,二面角![]() 是銳角,∴其余弦值為
是銳角,∴其余弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),在極坐標(與直角坐標系
為參數),在極坐標(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的方程為
的方程為![]()
(1)求圓![]() 的直角坐標方程;
的直角坐標方程;
(2)設圓![]() 與直線
與直線![]() 交于點
交于點![]() ,
,![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以O為極點,x軸的正半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() ;直線l的參數方程為
;直線l的參數方程為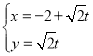 (t為參數).直線l與曲線C分別交于M,N兩點.
(t為參數).直線l與曲線C分別交于M,N兩點.
(1)寫出曲線C的直角坐標方程和直線l的普通方程;
(2)若點P的極坐標為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國式過馬路”存在很大的交通安全隱患,某調查機構為了解路人對“中國式過馬路”的態度是否與性別有關,從馬路旁隨機抽取30名路人進行了問卷調查,得到了如圖的![]() 列聯表.已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是
列聯表.已知在這30人中隨機抽取1人抽到反感“中國式過馬路”的路人的概率是![]() .
.
(1)求![]() 列聯表中的
列聯表中的![]() ,
,![]() 的值;
的值;
男性 | 女性 | 合計 | |
反感 | 10 |
|
|
不反感 |
| 8 |
|
合計 |
|
| 30 |
(2)根據列聯表中的數據,判斷是否有95%把握認為反感“中國式過馬路”與性別有關?
臨界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①![]() 的周期為
的周期為![]() ;
;
②![]() 在
在![]() 上單調遞增;
上單調遞增;
③函數![]() 在
在![]() 上有
上有![]() 個零點;
個零點;
④函數![]() 的最小值為
的最小值為![]() .
.
其中所有正確結論的編號為( )
A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在高一部分學生中調查男女同學對某項體育運動的喜好情況,其二維條形圖如圖(黑色代表喜好,白色代表不喜好).
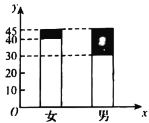
(1)寫出![]() 列聯表;
列聯表;
(2)能否有99%的把握認為喜好這項體育運動與性別有關;
(3)在這次調查中從喜好這項體育活動的一名男生和兩名女生中任選兩人進行專業培訓,求恰是一男一女的概率.
附: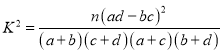
| 0.25 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com