
【題目】關(guān)于函數(shù)![]() 有下述四個(gè)結(jié)論:
有下述四個(gè)結(jié)論:
①![]() 的周期為
的周期為![]() ;
;
②![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
③函數(shù)![]() 在
在![]() 上有
上有![]() 個(gè)零點(diǎn);
個(gè)零點(diǎn);
④函數(shù)![]() 的最小值為
的最小值為![]() .
.
其中所有正確結(jié)論的編號為( )
A.①②B.②③C.③④D.②④
【答案】C
【解析】
利用特殊值法可判斷①的正誤;當(dāng)![]() 時(shí),化簡函數(shù)
時(shí),化簡函數(shù)![]() 的解析式,利用整體代入法驗(yàn)證函數(shù)
的解析式,利用整體代入法驗(yàn)證函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性,可判斷②的正誤;求得方程
上的單調(diào)性,可判斷②的正誤;求得方程![]() 在區(qū)間
在區(qū)間![]() 上的實(shí)數(shù)解,可判斷③的正誤;分別求出函數(shù)
上的實(shí)數(shù)解,可判斷③的正誤;分別求出函數(shù)![]() 在區(qū)間
在區(qū)間![]() 和
和![]() 上的最小值,比較大小后可判斷④的正誤.綜合可得出結(jié)論.
上的最小值,比較大小后可判斷④的正誤.綜合可得出結(jié)論.
對于①,![]() ,
,![]() ,
,
![]() ,
,![]() ,所以,函數(shù)
,所以,函數(shù)![]() 的周期不是
的周期不是![]() ,命題①錯(cuò)誤;
,命題①錯(cuò)誤;
對于②,當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() ,
,
所以,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上不單調(diào),命題②錯(cuò)誤;
上不單調(diào),命題②錯(cuò)誤;
對于③,![]() ,
,
且該函數(shù)的定義域?yàn)?/span>![]() ,則函數(shù)
,則函數(shù)![]() 為偶函數(shù),
為偶函數(shù),
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,
令![]() ,可得
,可得![]() 或
或![]() ,解得
,解得![]() 或
或![]() ,
,
由于函數(shù)![]() 為偶函數(shù),則方程
為偶函數(shù),則方程![]() 在區(qū)間
在區(qū)間![]() 上的實(shí)根為
上的實(shí)根為![]() .
.
所以,函數(shù)![]() 在
在![]() 上有
上有![]() 個(gè)零點(diǎn),命題③正確;
個(gè)零點(diǎn),命題③正確;
對于④,當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以,函數(shù)![]() 在
在![]() 上的最小值為
上的最小值為![]() ,
,
由于函數(shù)![]() 為
為![]() 上的增函數(shù),則該函數(shù)在
上的增函數(shù),則該函數(shù)在![]() 上的最小值為
上的最小值為![]() .
.
因此,函數(shù)![]() 的最小值為
的最小值為![]() ,命題④正確.
,命題④正確.
故選:C.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 、
、![]() 的值;
的值;
(2)設(shè)函數(shù)![]() ,
,![]() (其中
(其中![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
①當(dāng)![]() 時(shí),求
時(shí),求![]() 的最大值;
的最大值;
②若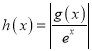 是單調(diào)遞減函數(shù),求實(shí)數(shù)
是單調(diào)遞減函數(shù),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn).
的中點(diǎn).
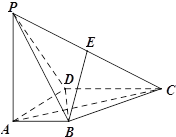
(1)證明:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 為棱
為棱![]() 上一點(diǎn),滿足
上一點(diǎn),滿足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的最值;
的最值;
(2)函數(shù)![]() 圖像在點(diǎn)
圖像在點(diǎn)![]() 處的切線斜率為
處的切線斜率為![]() 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() 、
、![]() ,且
,且![]() ,橢圓經(jīng)過點(diǎn)
,橢圓經(jīng)過點(diǎn)![]() .
.
(1)求橢圓的方程;
(2)直線![]() 過橢圓右頂點(diǎn)
過橢圓右頂點(diǎn)![]() ,交橢圓于另一點(diǎn)
,交橢圓于另一點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在直線
在直線![]() 上,且
上,且![]() .若
.若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為實(shí)常數(shù)).
為實(shí)常數(shù)).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若存在兩個(gè)不相等的正數(shù)![]() 、
、![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市環(huán)保部門對該市市民進(jìn)行了一次垃圾分類知識(shí)的網(wǎng)絡(luò)問卷調(diào)查,每位市民僅有一次參加機(jī)會(huì),通過隨機(jī)抽樣,得到參與問卷調(diào)查的100人的得分(滿分:100分)數(shù)據(jù),統(tǒng)計(jì)結(jié)果如表所示:
組別 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若規(guī)定問卷得分不低于70分的市民稱為“環(huán)保關(guān)注者”,請完成答題卡中的![]() 列聯(lián)表,并判斷能否在犯錯(cuò)誤概率不超過0.05的前提下,認(rèn)為是否為“環(huán)保關(guān)注者”與性別有關(guān)?
列聯(lián)表,并判斷能否在犯錯(cuò)誤概率不超過0.05的前提下,認(rèn)為是否為“環(huán)保關(guān)注者”與性別有關(guān)?
(2)若問卷得分不低于80分的人稱為“環(huán)保達(dá)人”.視頻率為概率.
①在我市所有“環(huán)保達(dá)人”中,隨機(jī)抽取3人,求抽取的3人中,既有男“環(huán)保達(dá)人”又有女“環(huán)保達(dá)人”的概率;
②為了鼓勵(lì)市民關(guān)注環(huán)保,針對此次的調(diào)查制定了如下獎(jiǎng)勵(lì)方案:“環(huán)保達(dá)人”獲得兩次抽獎(jiǎng)活動(dòng);其他參與的市民獲得一次抽獎(jiǎng)活動(dòng).每次抽獎(jiǎng)獲得紅包的金額和對應(yīng)的概率.如下表:
紅包金額(單位:元) | 10 | 20 |
概率 |
|
|
現(xiàn)某市民要參加此次問卷調(diào)查,記![]() (單位:元)為該市民參加間卷調(diào)查獲得的紅包金額,求
(單位:元)為該市民參加間卷調(diào)查獲得的紅包金額,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知矩形![]() 所在平面與
所在平面與![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() .
.

(1)若M為![]() 中點(diǎn),N為
中點(diǎn),N為![]() 中點(diǎn),證明:
中點(diǎn),證明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,且
,且![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com