
【題目】在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所對的邊分別為
所對的邊分別為![]() 、
、![]() 、
、![]() ,
,![]() ,當角
,當角![]() 取最大值時,
取最大值時,![]() 的周長為
的周長為![]() ,則
,則![]() __________.
__________.
【答案】3
【解析】分析:根據題意由正弦定理得出cosA<0,A為鈍角,cosAcosC≠0,由兩角和的正弦函數公式,同角三角函數基本關系式可得出tanA=﹣3tanC,且tanC>0;由已知及基本不等式求出B取得最大值,可得C=B=![]() ,可求A,利用余弦定理可求a=
,可求A,利用余弦定理可求a=![]() b,結合已知求得b的值,進而可求a的值.
b,結合已知求得b的值,進而可求a的值.
詳解:△ABC中,![]() sinB=cos(B+C)sinC,
sinB=cos(B+C)sinC,
∴![]() b=cos(B+C)c,即cosA=﹣
b=cos(B+C)c,即cosA=﹣![]() <0,∴A為鈍角,
<0,∴A為鈍角,
∴cosAcosC≠0;
由sinB=sin(A+C)=sinAcosC+cosAsinC=﹣2cosAsinC,
可得tanA=﹣3tanC,且tanC>0,
![]()
=![]()
當且僅當tanC=![]() 時取等號;
時取等號;
∴B取得最大值時,c=b=1,此時C=B=![]() .
.
∴A=![]() ,由a2=b2+c2﹣2bccosA,可得:a=
,由a2=b2+c2﹣2bccosA,可得:a=![]() b,
b,
∵三角形的周長為a+b+c=![]() b +b+b=2
b +b+b=2![]() .解得:b=
.解得:b=![]() ,可得:a=
,可得:a=![]() b =3.
b =3.
故答案為:3


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
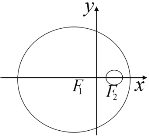
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動圓
,若動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切.
外切.
(Ⅰ)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過直線![]() 上的點
上的點![]() 作圓
作圓![]() 的兩條切線,設切點分別是
的兩條切線,設切點分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
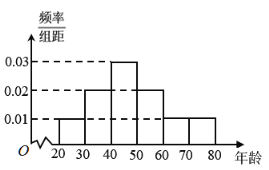
【題目】退休年齡延遲是平均預期壽命延長和人口老齡化背景下的一種趨勢.某機構為了了解某城市市民的年齡構成,從該城市市民中隨機抽取年齡段在[20,80]內的600人進行調查,并按年齡層次繪制頻率分布直方圖,如圖所示.若規定年齡分布在[60,80]內的人為“老年人”,將上述人口分布的頻率視為該城市年齡段在[20,80]的人口分布的概率.從該城市年齡段在[20,80]內的市民中隨機抽取3人,記抽到“老年人”的人數為![]() 則隨機變量
則隨機變量![]() 的數學期望為______.
的數學期望為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數
,求實數![]() 、
、![]() 的值;
的值;
(2)設函數![]() ,
,![]() (其中
(其中![]() 為自然對數的底數).
為自然對數的底數).
①當![]() 時,求
時,求![]() 的最大值;
的最大值;
②若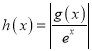 是單調遞減函數,求實數
是單調遞減函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行促銷活動,有兩個摸獎箱,![]() 箱內有一個“
箱內有一個“![]() ”號球,兩個“
”號球,兩個“![]() ”號球,三個“
”號球,三個“![]() ”號球、四個無號球,
”號球、四個無號球,![]() 箱內有五個“
箱內有五個“![]() ”號球,五個“
”號球,五個“![]() ”號球,每次摸獎后放回,每位顧客消費額滿
”號球,每次摸獎后放回,每位顧客消費額滿![]() 元有一次
元有一次![]() 箱內摸獎機會,消費額滿
箱內摸獎機會,消費額滿![]() 元有一次
元有一次![]() 箱內摸獎機會,摸得有數字的球則中獎,“
箱內摸獎機會,摸得有數字的球則中獎,“![]() ”號球獎
”號球獎![]() 元,“
元,“![]() ”號球獎
”號球獎![]() 元,“
元,“![]() ”號球獎
”號球獎![]() 元,摸得無號球則沒有獎金。
元,摸得無號球則沒有獎金。
(1)經統計,顧客消費額![]() 服從正態分布
服從正態分布![]() ,某天有
,某天有![]() 位顧客,請估計消費額
位顧客,請估計消費額![]() (單位:元)在區間
(單位:元)在區間![]() 內并中獎的人數.(結果四舍五入取整數)
內并中獎的人數.(結果四舍五入取整數)
附:若![]() ,則
,則![]() ,
,![]() .
.
(2)某三位顧客各有一次![]() 箱內摸獎機會,求其中中獎人數
箱內摸獎機會,求其中中獎人數![]() 的分布列.
的分布列.
(3)某顧客消費額為![]() 元,有兩種摸獎方法,
元,有兩種摸獎方法,
方法一:三次![]() 箱內摸獎機會;
箱內摸獎機會;
方法二:一次![]() 箱內摸獎機會.
箱內摸獎機會.
請問:這位顧客選哪一種方法所得獎金的期望值較大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一家商場銷售一種商品,該商品一天的需求量在![]() 范圍內等可能取值,該商品的進貨量也在
范圍內等可能取值,該商品的進貨量也在![]() 范圍內取值(每天進貨1次).這家商場每銷售一件該商品可獲利60元;若供不應求,可從其他商店調撥,銷售一件該商品可獲利40元;若供大于求,剩余的每處理一件該商品虧損20元.設該商品每天的需求量為
范圍內取值(每天進貨1次).這家商場每銷售一件該商品可獲利60元;若供不應求,可從其他商店調撥,銷售一件該商品可獲利40元;若供大于求,剩余的每處理一件該商品虧損20元.設該商品每天的需求量為![]() ,每天的進貨量為
,每天的進貨量為![]() 件,該商場銷售該商品的日利潤為
件,該商場銷售該商品的日利潤為![]() 元.
元.
(1)寫出這家商場銷售該商品的日利潤為![]() 關于需求量
關于需求量![]() 的函數表達式;
的函數表達式;
(2)寫出供大于求,銷售![]() 件商品時,日利潤
件商品時,日利潤![]() 的分布列;
的分布列;
(3)當進貨量![]() 多大時,該商場銷售該商品的日利潤的期望值最大?并求出日利潤的期望值的最大值.
多大時,該商場銷售該商品的日利潤的期望值最大?并求出日利潤的期望值的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com