
分析 (1)直接由指數函數的單調性,求得x的取值范圍;
(2)由(1)中求得的x的范圍,得到log2x的范圍,令t=log2x換元,再由二次函數的圖象和性質求得函數$y=({log_2}^x-1)({log_2}^x+3)$的值域.
解答 解:(1)∵$\sqrt{3}≤{3^x}≤9$,
∴${3^{\frac{1}{2}}}≤{3^x}≤{3^2}$,
由于指數函數y=3x在R上單調遞增,
∴$\frac{1}{2}≤x≤2$;
(2)由(1)得$\frac{1}{2}≤x≤2$,
∴-1≤log2x≤1,
令t=log2x,則y=(t-1)(t+3)=t2+2t-3,其中t∈[-1,1],
∵函數y=t2+2t-3開口向上且對稱軸為t=-1,
∴函數y=t2+2t-3在t∈[-1,1]上單調遞增,
∴y的最大值為f(1)=0,最小值為f(-1)=-4.
∴函數y=(log2x-1)(log2x+3)的值域為[-4,0].
點評 本題考查指數不等式的解法,訓練了函數值域的求法,屬中檔題.


 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
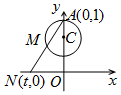 如圖,周長為1的圓的圓心C在y軸上,一動點M從圓上的點A(0,1)開始按逆時針方向繞圓運動一周,記走過的弧長為x,直線AM與x軸交于點N(t,0),則函數t=f(x)的圖象大致為( )
如圖,周長為1的圓的圓心C在y軸上,一動點M從圓上的點A(0,1)開始按逆時針方向繞圓運動一周,記走過的弧長為x,直線AM與x軸交于點N(t,0),則函數t=f(x)的圖象大致為( )| A. | 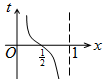 | B. | 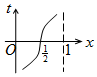 | C. | 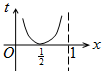 | D. | 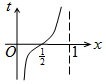 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | a<c<b |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com