Question

13．等腰三角形ABC中，AB=4，AC=BC=3，點E，F(xiàn)分別位于兩腰上，E，F(xiàn)將△ABC分成周長相等的三角形與四邊形，面積分別為S₁，S₂，則$\frac{S_1}{S_2}$的最大值為$\frac{25}{11}$．

Answer 1

分析 根據(jù)條件畫出圖象，由圖求出底邊上的高和sinA的值，由正弦定理求出sinC，設CE=x，CF=y，利用三角形的面積公式求出S₁和S₂=S_三角形ABC-S₁，由條件列出方程化簡后，根據(jù)基本不等式求出xy的范圍，代入$\frac{{S}_{1}}{{S}_{2}}$化簡后求出$\frac{S_1}{S_2}$的最大值．

解答 解：設E、F分別在AC和BC上，如圖所示：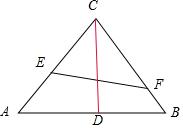
取AB的中點D，連接CD，
∵AB=4，AC=BC=3，∴CD=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$，
則sinA=$\frac{CD}{AC}$=$\frac{\sqrt{5}}{3}$，
由$\frac{BC}{sinA}=\frac{AB}{sinC}$得，sinC=$\frac{ABsinA}{BC}$=$\frac{4×\frac{\sqrt{5}}{3}}{3}$=$\frac{4\sqrt{5}}{9}$，
設CE=x，CF=y，所以S₁=$\frac{1}{2}$xysinC=$\frac{2\sqrt{5}}{9}xy$，
則S₂=S_三角形ABC-S₁=2$\sqrt{5}$-S₁=$2\sqrt{5}-\frac{2\sqrt{5}}{9}xy$，
由條件得x+y=3-x+4-y+3，化簡得x+y=5，
則xy≤$（\frac{x+y}{2}）^{2}$=$\frac{25}{4}$，當且僅當x=y=$\frac{5}{2}$ 時取等號，
所以$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{2\sqrt{5}}{9}xy}{2\sqrt{5}-\frac{2\sqrt{5}}{9}xy}$=$\frac{xy}{9-xy}$=$\frac{1}{\frac{9}{xy}-1}$≤$\frac{1}{\frac{36}{25}-1}$=$\frac{25}{11}$，
當且僅當x=y=$\frac{5}{2}$ 時取等號，
則$\frac{S_1}{S_2}$的最大值是$\frac{25}{11}$，
故答案為：$\frac{25}{11}$．

點評 本題考查了基本不等式在實際問題中的應用，正弦定理，以及三角形的面積公式，考查化簡、變形能力．