Question

【題目】某校高一年級學生全部參加了體育科目的達標測試,現從中隨機抽取40名學生的測試成績,整理數據并按分數段進行分組,假設同一組中的每個數據可用該組區間的中點值代替,則得到體育成績的折線圖如圖.

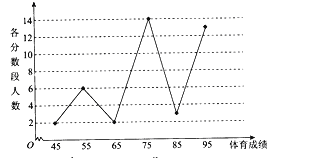
(1)體育成績大于或等于70分的學生常被稱為“體育良好”.已知該校高一年級有1000名學生,試估計高一年級中“體育良好”的學生人數;

(2)為分析學生平時的體育活動情況,現從體育成績在和的樣本學生中隨機抽取2人,求在抽取的2名學生中,至少有1人體育成績在的概率.

Answer 1

【答案】(1) 人(2)

【解析】試題分析：（1）由折線圖知，樣本中體育成績大于或等于70分的學生有，所以“體育良好”的學生人數大約為（2）體育成績在和的樣本學生共有5人，利用枚舉法可得從這兩組學生中隨機抽取2人，所有可能的結果為10種，其中體育成績在皆在有3種，即至少有1人體育成績在有7種，因此根據古典概型概率計算方法得概率為

試題解析：（1）由折線圖知，樣本中體育成績大于或等于70分的學生有30人，所以該校高一年級學生中，“體育良好”的學生人數大約為人．

（2）設“至少有1人體育成績 在為事件，記體育成績 在的學生為，體育成績在的學生為，則從這兩組學生中隨機抽取2人，所有可能的結果如下：

共10種，

而事件所包含的結果有共7種，因此事件發生的概率為．