【題目】已知直線
過坐標原點
，圓
的方程為
．
（1）當直線
的斜率為
時，求
與圓
相交所得的弦長；
（2）設直線
與圓
交于兩點
，且
為
的中點，求直線
的方程．
【答案】(1) 
;(2) 直線l的方程為y=x或y=﹣x.
【解析】試題分析：(1) 由已知，直線
的方程為
，圓
圓心為
，半徑為
，求出圓心到直線
的距離，根據勾股定理可求
與圓
相交所得的弦長；（2）設直線
與圓
交于兩點
，且
為
的中點，設
，則
，將
點的坐標代入橢圓方程求出
的坐標，即可求直線
的方程.
試題解析：（1）由已知，直線l的方程為y=
x，圓C圓心為（0，3），半徑為
，
所以，圓心到直線l的距離為
=
．…
所以，所求弦長為2
=2．
（2） 設A（x1，y1），因為A為OB的中點，則B（2x1，2y1）．
又A，B在圓C上，
所以 x12+y12﹣6y1+4=0，4x12+4y12﹣12y1+4=0．
解得y1=1，x1=±1，
即A（1，1）或A（﹣1，1）
所以，直線l的方程為y=x或y=﹣x．
科目：高中數學 來源： 題型：
【題目】松江有軌電車項目正在如火如荼的進行中，通車后將給市民出行帶來便利，已知某條線路通車后，電車的發車時間間隔t（單位：分鐘）滿足
，市場調研測試，電車載客量與發車時間間隔t相關，當
時電車為滿載狀態，載客為400人，當
時，載客量會少，少的人數與
的平方成正比，且發車時間間隔為2分鐘時的載客為272人，記電車載客為
．
（1）求的表達式；
（2）若該線路分鐘的凈收益為
（元），問當發車時間間隔為多少時，該線路每分鐘的凈收益最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】國慶期間，某旅行社組團去風景區旅游，若旅行團人數不超過20人，每人需交費用800元；若旅行團人數超過20人，則給予優惠：每多1人，人均費用減少10元，直到達到規定人數60人為止.旅行社需支付各種費用共計10000元.
（1）寫出每人需交費用S關于旅行團人數
的函數；
（2）旅行團人數x為多少時，旅行社可獲得最大利潤？最大利潤是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高一年級學生全部參加了體育科目的達標測試,現從中隨機抽取40名學生的測試成績,整理數據并按分數段
進行分組,假設同一組中的每個數據可用該組區間的中點值代替,則得到體育成績的折線圖如圖.
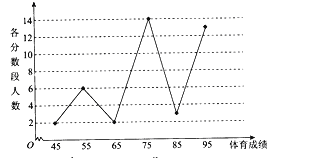
(1)體育成績大于或等于70分的學生常被稱為“體育良好”.已知該校高一年級有1000名學生,試估計高一年級中“體育良好”的學生人數;
(2)為分析學生平時的體育活動情況,現從體育成績在
和
的樣本學生中隨機抽取2人,求在抽取的2名學生中,至少有1人體育成績在
的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對任意實數
，
，
，給出下列命題，其中真命題是（ ）
A.“
”是“
”的充要條件B.“
”是“
”的充分條件
C.“
”是“
”的必要條件D.“
是無理數”是“是無理數”的充要條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
是拋物線為
上的一點，以S為圓心，r為半徑
做圓，分別交x軸于A，B兩點，連結并延長SA、SB，分別交拋物線于C、D兩點．
求拋物線的方程．
求證：直線CD的斜率為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正四棱錐
的側棱和底面邊長相等，在這個正四棱錐的
條棱中任取兩條，按下列方式定義隨機變量
的值：
若這兩條棱所在的直線相交，則
的值是這兩條棱所在直線的夾角大小（弧度制）；
若這兩條棱所在的直線平行，則
；
若這兩條棱所在的直線異面，則
的值是這兩條棱所在直線所成角的大小(弧度制).
（1）求
的值；
（2）求隨機變量
的分布列及數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為偶函數．
（1）求實數
的值，并寫出
在區間
上的增減性和值域（不需要證明）；
（2）令
，其中
，若
對任意
、
，總有
，求
的取值范圍；
（3）令
，若
對任意、
，總有
，求實數
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
