【題目】已知函數
(I)若函數
處取得極值，求實數
的值；并求此時
上的最大值；
(Ⅱ)若函數
不存在零點，求實數a的取值范圍；
【答案】（1）最大值為
；（2）實數
的取值范圍是
。
【解析】試題分析：（1）根據函數的極值的概念得到
， 
，根據函數的單調性得到函數的最值。（2）研究函數的單調性，找函數和軸的交點，使得函數和軸沒有交點即可；分
和
，兩種情況進行討論。
解析：
（1）函數
的定義域為R， 
，
， 
.
在
上
單調遞減，在
上
單調遞增，所以
時
取極小值.
所以所求實數
的值為1.
易知
在
上
單調遞增，在
上
單調遞減；
且
.
當
時， 
在
的最大值為
（2）
，由于
.
①當
時， 
是增函數，
且當
時， 
.
當
時， 
， 
，取
，
則
，所以函數
存在零點.
②當
時， 
.
在
上
單調遞減，在
上
單調遞增，所以
時
取最小值.
函數
不存在零點，等價于
，
解得
.
綜上所述：所求的實數
的取值范圍是
.
黃岡冠軍課課練系列答案科目：高中數學 來源： 題型：
【題目】
已知橢圓C： 
(a>b>0)的左、右焦點分別為F1，F2，離心率為
，直線y＝x＋b截得橢圓C的弦長為
.
(Ⅰ)求橢圓C的方程；
(Ⅱ)過點(m,0)作圓x2＋y2＝1的切線，交橢圓C于點A，B，求|AB|的最大值，并求取得最大值時m的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f(x)＝a
－2ln x(a∈R)．
(Ⅰ)當a＝2時，求曲線f(x)在x＝2處的切線方程；
(Ⅱ)若a>
，且m，n分別為f(x)的極大值和極小值，S＝m－n，求證：S<
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線C的極坐標方程是ρ＝2,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,直線l的參數方程為
(t為參數).
(1)寫出直線l的普通方程與曲線C的直角坐標方程;
(2)設曲線C經過伸縮變換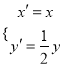
得到曲線,設M(x,y)為
上任意一點,求
的最小值,并求相應的點M的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗，苗主責之粟五斗，羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之，問各出幾何？此問題的譯文是:今有牛、馬、羊吃了別人的禾苗，禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還，他們各應償還多少？已知牛、馬、羊的主人各應償還
升， 
升， 
升，1斗為10升，則下列判斷正確的是( )
A. 
， 
， 
依次成公比為2的等比數列，且
B. 
， 
， 
依次成公比為2的等比數列，且
C. 
， 
， 
依次成公比為
的等比數列，且
D. 
， 
， 
依次成公比為
的等比數列，且
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856263)
已知拋物線y2＝2px(p>0)的準線與x軸交于點N，過點N作圓M：(x－2)2＋y2＝1的兩條切線，切點為P、Q，且|PQ|＝
.
(Ⅰ)求拋物線的方程；
(Ⅱ)過拋物線的焦點F作斜率為k1的直線與拋物線交于A、B兩點，A、B兩點的橫坐標均不為2，連接AM，BM并延長分別交拋物線于C、D兩點，設直線CD的斜率為k2，問
是否為定值？若是，求出該定值；若不是，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856288)
設函數f(x)＝aln x－x，g(x)＝aex－x，其中a為正實數．
(Ⅰ)若f(x)在(1，＋∞)上是單調減函數，且g(x)在(2，＋∞)上有最小值，求a的取值范圍；
(Ⅱ)若函數f(x)與g(x)都沒有零點，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856295)德國大數學家高斯年少成名，被譽為數學王子.19歲的高斯得到了一個數學史上非常重要的結論，就是《正十七邊形尺規作圖之理論與方法》， 在其年幼時，對1＋2＋3＋…＋100的求和運算中，提出了倒序相加法的原理，該原理基于所給數據前后對應項的和呈現一定的規律生成，因此，此方法也被稱為高斯算法．現有函數f(x)＝
，則f(1)＋f(2)＋…＋f(m＋2017)等于( )
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
