
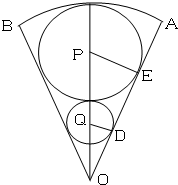
 如圖,在半徑為2,圓心角為變量的扇形OAB內作一內切圓P,再在扇形內作一個與扇形兩半徑相切并與圓P外切的小圓Q,設圓P與圓Q的半徑之積為y.
如圖,在半徑為2,圓心角為變量的扇形OAB內作一內切圓P,再在扇形內作一個與扇形兩半徑相切并與圓P外切的小圓Q,設圓P與圓Q的半徑之積為y.分析 (1)①設圓P與圓Q的半徑分別為R、r.由R=(2-R)•sinθ得$R=\frac{2sinθ}{1+sinθ}$,由此能將y表示成θ的函數.
②圓Q的半徑為r,由$\frac{r}{x}=\frac{2-2x-r}{2-x}$,能將y表示成x的函數.
(2)選擇②:由y=-x3+x2(0<x<1)得y'=-3x2+2x(0<x<1),由此利用導數性質能求出y的最大值.
解答 解:(1)①如圖,設圓P與圓Q的半徑分別為R、r.
由R=(2-R)•sinθ得$R=\frac{2sinθ}{1+sinθ}$,
又$\frac{r}{R}=\frac{2-2R-r}{2-R}$,
∴$r=R-{R^2}=\frac{2sinθ}{1+sinθ}-{(\frac{2sinθ}{1+sinθ})^2}=\frac{2sinθ•(1-sinθ)}{{{{(1+sinθ)}^2}}}$,
∴$y=r•R=\frac{{4{{sin}^2}θ({1-sinθ})}}{{{{({1+sinθ})}^3}}}(0<θ<\frac{π}{2})$.(5分)
②圓Q的半徑為r,由$\frac{r}{x}=\frac{2-2x-r}{2-x}$得r=x-x2,
∴y=r•x=-x3+x2(0<x<1).(10分)
(2)選擇②:由y=-x3+x2(0<x<1)得y'=-3x2+2x(0<x<1),
令y'>0,得$0<x<\frac{2}{3}$; 令y'<0,得$\frac{2}{3}<x<1$.
∴y=-x3+x2(0<x<1)在區間$(0,\frac{2}{3})$上是增函數,在區間$(\frac{2}{3},1)$上是減函數.
∴當$x=\frac{2}{3}$時,${y_{max}}=\frac{4}{27}$.(15分)
點評 本題考查函數解析式的求法,考查函數值的最大值的求法,是中檔題,解題時要認真審題,注意導數性質的合理運用.


 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -2 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com