
【題目】設Sn是數列{an}的前n項和,且2an+Sn=An2+Bn+C.
(1)當A=B=0,C=1時,求an;
(2)若數列{an}為等差數列,且A=1,C=﹣2. ①設bn=2nan , 求數列{bn}的前n項和;
②設cn= ![]() ,若不等式cn≥
,若不等式cn≥ ![]() 對任意n∈N*恒成立,求實數m的取值范圍.
對任意n∈N*恒成立,求實數m的取值范圍.
【答案】
(1)解:當A=B=0,C=1時,2an+Sn=1,
∴ ![]() ;
;
當n≥2時,2an﹣1+Sn﹣1=1,
兩式作差得:3an=2an﹣1,即 ![]() ,
,
∴數列{an}是以 ![]() 為首項,以
為首項,以 ![]() 為公比的等比數列,
為公比的等比數列,
∴ ![]()
(2)解:當A=1,C=﹣2時,2an+Sn=n2+Bn﹣2,
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∵數列{an}為等差數列,
∴ ![]() ,解得:B=4.
,解得:B=4.
∴a1=1,a2=5,則d=4,
∴an=1+4(n﹣1)=4n﹣3,
① bn=2nan=(4n﹣3)2n,
∴數列{bn}的前n項和 ![]() ,
,
![]() ,
,
兩式作差得: ![]()
= ![]() =2﹣16+2n+3﹣(4n﹣3)2n+1,
=2﹣16+2n+3﹣(4n﹣3)2n+1,
∴ ![]() ;
;
②cn= ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() 單調遞增,
單調遞增,
∴當n=1時, ![]() 有最小值為
有最小值為 ![]() ,
,
∴ ![]() ,即m≤﹣14.
,即m≤﹣14.
∴實數m的取值范圍是(﹣∞,﹣14]
【解析】(1)把A=B=0,C=1代入2an+Sn=An2+Bn+C,求得數列首項,進一步可得數列{an}是以 ![]() 為首項,以
為首項,以 ![]() 為公比的等比數列,則數列的通項公式可求;(2)①由已知求出B,得到數列{an}的通項公式,代入bn=2nan , 利用錯位相減法求得數列{bn}的前n項和Tn;②把Tn代入cn=
為公比的等比數列,則數列的通項公式可求;(2)①由已知求出B,得到數列{an}的通項公式,代入bn=2nan , 利用錯位相減法求得數列{bn}的前n項和Tn;②把Tn代入cn= ![]() ,由函數的單調性求其最小值,由
,由函數的單調性求其最小值,由 ![]() 小于等于cn的最小值求得m的取值范圍.
小于等于cn的最小值求得m的取值范圍.
【考點精析】通過靈活運用等差數列的通項公式(及其變式)和數列的前n項和,掌握通項公式:![]() 或
或![]() ;數列{an}的前n項和sn與通項an的關系
;數列{an}的前n項和sn與通項an的關系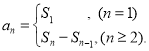 即可以解答此題.
即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知△ABC的角A、B、C所對的邊分別是a、b、c,設向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求證:△ABC為等腰三角形;
,求證:△ABC為等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,邊長c=2,角C=
,邊長c=2,角C= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校用簡單隨機抽樣方法抽取了30名同學,對其每月平均課外閱讀時間(單位:小時)進行調查,莖葉圖如圖:
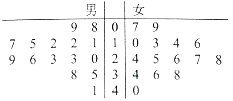
若將月均課外閱讀時間不低于30小時的學生稱為“讀書迷”.
(1)將頻率視為概率,估計該校900名學生中“讀書迷”有多少人?
(2)從已抽取的7名“讀書迷”中隨機抽取男、女“讀書迷”各1人,參加讀書日宣傳活動.
(i)共有多少種不同的抽取方法?
(ii)求抽取的男、女兩位“讀書迷”月均讀書時間相差不超過2小時的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某市2017年3月1日至16日的空氣質量指數趨勢圖,空氣質量指數![]() 小于
小于![]() 表示空氣質量優良,空氣質量指數大于
表示空氣質量優良,空氣質量指數大于![]() 表示空氣重度污染.
表示空氣重度污染.
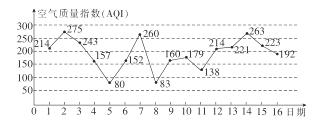
(1)若該人隨機選擇3月1日至3月14日中的某一天到達該市,到達后停留![]() 天(到達當日算
天(到達當日算![]() 天),求此人停留期間空氣重度污染的天數為
天),求此人停留期間空氣重度污染的天數為![]() 天的概率;
天的概率;
(2)若該人隨機選擇3月7日至3月12日中的![]() 天到達該市,求這
天到達該市,求這![]() 天中空氣質量恰有
天中空氣質量恰有![]() 天是重度污染的概率.
天是重度污染的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=3sin(2x+ ![]() )的圖象為C,關于函數f(x)及其圖象的判斷如下: ①圖象C關于點(
)的圖象為C,關于函數f(x)及其圖象的判斷如下: ①圖象C關于點( ![]() ,0)對稱;
,0)對稱;
②圖象C關于直線x= ![]() 對稱;
對稱;
③由圖象C向右平移 ![]() 個單位長度可以得到y=3sin2x的圖象;
個單位長度可以得到y=3sin2x的圖象;
④函數f(x)在區間(﹣ ![]() ,
, ![]() )內是減函數;
)內是減函數;
⑤函數|f(x)+1|的最小正周期為 ![]() .
.
其中正確的結論序號是 . (把你認為正確的結論序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三角形ABC中,分別根據下列條件解三角形,其中有兩個解的是( )
A.a=8b=16A=30°
B.a=25b=30A=150°
C.a=30b=40A=30°
D.a=72b=60A=135°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一鮮花店根據一個月(30天)某種鮮花的日銷售量與銷售天數統計如下,將日銷售量落入各組區間頻率視為概率.
日銷售量(枝) |
|
|
|
|
|
銷售天數 | 3天 | 5天 | 13天 | 6天 | 3天 |
(1)試求這30天中日銷售量低于100枝的概率;
(2)若此花店在日銷售量低于100枝的時候選擇2天作促銷活動,求這2天恰好是在日銷售量低于50枝時的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com