
【題目】已知圓![]() 過
過![]() ,
, ![]() 兩點,且圓心
兩點,且圓心![]() 在直線
在直線![]() 上.
上.
(1)求圓![]() 的方程;
的方程;
(2)若直線![]() 過點
過點![]() 且被圓
且被圓![]() 截得的線段長為
截得的線段長為![]() ,求
,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】試題分析:(1)把點P、Q的坐標和圓心坐標代入圓的一般方程,利用待定系數法求得系數的值;(2)分類討論,斜率存在和斜率不存在兩種情況.①當直線l的斜率不存在時,滿足題意,易得直線方程;②當直線l的斜率存在時,設所求直線l的斜率為k,則直線l的方程為:y-5=kx,由點到直線的距離公式求得k的值.
試題解析:
(1)設圓的方程為![]() ,圓心
,圓心![]() ,根據題意有
,根據題意有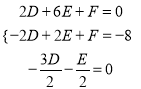 ,計算得出
,計算得出 ,
,
故所求圓的方程為![]() .
.
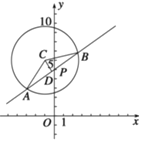
(2)如圖所示, ![]() ,設
,設![]() 是線段
是線段![]() 的中點,
的中點,
則![]() ,
,
∴![]() ,
, ![]() .
.
在![]() 中,可得
中,可得![]() .
.
當直線![]() 的斜率不存在時,滿足題意,
的斜率不存在時,滿足題意,
此時方程為![]() .
.
當直線![]() 的斜率存在時,設所求直線
的斜率存在時,設所求直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() 的方程為:
的方程為: ![]() ,
,
即![]() ,由點
,由點![]() 到直線
到直線![]() 的距離公式:
的距離公式:
![]() ,得
,得![]() ,此時直線
,此時直線![]() 的方程為
的方程為![]() .
.
∴所求直線![]() 的方程為
的方程為![]() 或
或![]()


科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸),一位居民的月用水量不超過
(噸),一位居民的月用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照
的部分按議價收費,為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照![]() ,
, ![]() ,…,
,…, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
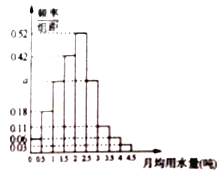
(1)求直方圖中![]() 的值;
的值;
(2)若將頻率視為概率,從該城市居民中隨機抽取3人,記這3人中月均用水量不低于3噸的人數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
(3)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值(精確到0.01),并說明理由.
的值(精確到0.01),并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設Sn是數列{an}的前n項和,且2an+Sn=An2+Bn+C.
(1)當A=B=0,C=1時,求an;
(2)若數列{an}為等差數列,且A=1,C=﹣2. ①設bn=2nan , 求數列{bn}的前n項和;
②設cn= ![]() ,若不等式cn≥
,若不等式cn≥ ![]() 對任意n∈N*恒成立,求實數m的取值范圍.
對任意n∈N*恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某算法的程序圖如圖所示,其中輸入的變量x在1,2,3,…,30這30個整數中等可能隨機產生. 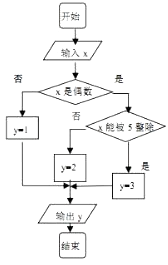
(1)分別求出按程序框圖正確編程運行時輸出y的值為i的概率Pi(i=1,2,3);
(2)甲、乙兩同學依據自己對程序框圖的理解,各自編寫程序重復運行n次后,統計記錄了輸出y的值為i(i=1,2,3)的頻數,下面是甲、乙所作頻數統計表的部分數據: 甲的頻數統計表(部分)
運行次數 | 輸出y=1的頻數 | 輸出y=2的頻數 | 輸出y=3的頻數 |
50 | 24 | 19 | 7 |
… | … | … | … |
2000 | 1027 | 776 | 197 |
乙的頻數統計表(部分)
運行次數 | 輸出y=1的頻數 | 輸出y=2的頻數 | 輸出y=3的頻數 |
50 | 26 | 11 | 13 |
… | … | … | … |
2000 | 1051 | 396 | 553 |
當n=2000時,根據表中的數據,分別寫出甲、乙所編程序各自輸出y的值為i(i=1,2,3)的頻率(用分數表示),并判斷甲、乙中誰所編寫的程序符合算法要求的可能性較大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的方程:x2+y2﹣4x﹣6y+m=0,若圓C與直線a:x+2y﹣3=0相交于M、N兩點,且|MN|=2 ![]() .
.
(1)求m的值;
(2)是否存在直線l:x﹣y+c=0,使得圓上有四點到直線l的距離為 ![]() ,若存在,求出c的范圍;若不存在,請說明理由.
,若存在,求出c的范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
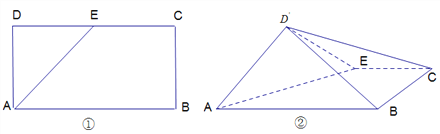
【題目】如圖①,在矩形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中點,將三角形
的中點,將三角形![]() 沿
沿![]() 翻折到圖②的位置,使得平面
翻折到圖②的位置,使得平面![]() 平面
平面![]() .
.
(Ⅰ)在線段![]() 上確定點
上確定點![]() ,使得
,使得![]() 平面
平面![]() ,并證明;
,并證明;
(Ⅱ)求![]() 與
與![]() 所在平面構成的銳二面角的正切值.
所在平面構成的銳二面角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸,焦距為2,且長軸長是短軸長的
軸,焦距為2,且長軸長是短軸長的![]() 倍.
倍.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設![]() ,過橢圓
,過橢圓![]() 左焦點
左焦點![]() 的直線
的直線![]() 交
交![]() 于
于![]() 、
、![]() 兩點,若對滿足條件的任意直線
兩點,若對滿足條件的任意直線![]() ,不等式
,不等式![]() (
(![]() )恒成立,求
)恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名高二文科生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班進行教改實驗.為了了解教學效果,期末考試后,陳老師對甲、乙兩個班級的學生成績進行統計分析,畫出頻率分布直方圖(如下圖).記成績不低于90分者為“成績優秀”.
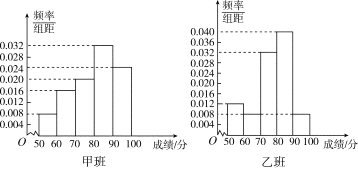
(Ⅰ)根據頻率分布直方圖填寫下面2×2列聯表;
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
(Ⅱ)判斷能否在犯錯誤的概率不超過0.05的前提下認為:“成績優秀”與教學方式有關?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com