
分析 (1)利用數列的通項公式以及已知條件列出方程組,求出公差與公比,然后求解通項公式.
(2)利用錯位相減法轉化求解數列的和即可.
解答 解:(1)設{an}是公差為d的等差數列,{bn}是公比為q的等比數列.
由題意$\left\{\begin{array}{l}{q^2}(3+3d)=36\\ q(2+d)=8\end{array}\right.⇒\left\{\begin{array}{l}d=2\\ q=2\end{array}\right.$或$\left\{\begin{array}{l}d=-\frac{2}{3}\\ q=6\end{array}\right.$,
所以an=2n-1,${b_n}={2^{n-1}}$或${a_n}=\frac{1}{3}(5-2n)$,${b_n}={6^{n-1}}$.
(2)若an<an+1,由(1)知an=2n-1,
∴$\frac{1}{anan+1}=\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$
∴${T_n}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+$…$+\frac{1}{2n-1}-\frac{1}{2n+1})=\frac{n}{2n+1}$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
點評 本題考查數列的遞推關系式的應用,數列求和,考查計算能力.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{3\sqrt{17}}}{17}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{17}}}{34}$ | D. | $\frac{{2\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
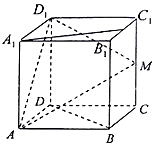 如圖邊長為2的正方體ABCD-A1B1C1D1中,M、N分別是CC1,B1C1的中點.
如圖邊長為2的正方體ABCD-A1B1C1D1中,M、N分別是CC1,B1C1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com