【題目】已知函數
，其中
，
且
，
且
.
（1）若
，試判斷
的奇偶性；
（2）若
，
，
，證明
的圖像是軸對稱圖形，并求出對稱軸.
【答案】(1)見解析（2）函數
的圖像是軸對稱圖形，其對稱軸是直線
．
【解析】
（1）由
得出
，于是得出
，利用偶函數的定義得出
，利用奇函數的定義得出
，于是得出當
時，函數
為非奇非偶函數；
（2）先得出
，并設函數圖象的對稱軸為直線
，利用定義
，列等式求出
的值，即可而出函數圖象的對稱軸方程.
（1）由已知，
，于是，則
，
若
是偶函數，則
，即
，
所以
對任意實數
恒成立，所以．
若是奇函數，則
，即
，
所以
對任意實數恒成立，所以．
綜上，當時，是偶函數；
當時，奇函數，當，既不是奇函數也不是偶函數；
（2），若函數的圖像是軸對稱圖形，且對稱軸是直線，即對任意實數，恒成立，
，化簡得
，
因為上式對任意
成立，所以
，
，
．
所以，函數的圖像是軸對稱圖形，其對稱軸是直線．
小學教材全測系列答案科目：高中數學 來源： 題型：
【題目】《最強大腦》是大型科學競技類真人秀節目，是專注傳播腦科學知識和腦力競技的節目．某機構為了了解大學生喜歡《最強大腦》是否與性別有關，對某校的100名大學生進行了問卷調查，得到如下列聯表：
喜歡《最強大腦》 | 不喜歡《最強大腦》 | 合計 | |
男生 | 15 | ||
女生 | 15 | ||
合計 |
已知在這100人中隨機抽取1人抽到不喜歡《最強大腦》的大學生的概率為0.4
（I）請將上述列聯表補充完整；判斷是否有99.9%的把握認為喜歡《最強大腦》與性別有關，并說明理由；
（II）已知在被調查的大學生中有5名是大一學生，其中3名喜歡《最強大腦》，現從這5名大一學生中隨機抽取2人，抽到喜歡《最強大腦》的人數為X，求X的分布列及數學期望．
參考公式：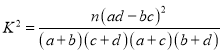
，
參考數據：
，
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】PM2．5是指大氣中直徑小于或等于2．5微米的顆粒物，也稱為可吸入肺顆粒物．我國PM2．5標準采用世衛組織設定的最寬限值，即PM2．5日均值在35微克/立方米以下空氣質量為一級；在35微克/立方米～75微克/立方米之間空氣質量為二級；在75微克/立方米以上空氣質量為超標．
某試點城市環保局從該市市區2015年全年每天的PM2．5監測數據中隨機抽取15天的數據作為樣本，監測值如莖葉圖所示(十位為莖，個位為葉)
(1)求中位數．
(2)從這15天的數據中任取兩天數據，記ξ表示抽到PM2．5監測數據超標的天數，求ξ的分布列及數學期望．
(3)以這15天的PM2．5日均值來估計一年的空氣質量情況，則一年(按360天計算)中平均有多少天的空氣質量達到一級或二級．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合
由滿足下列兩個條件的數列
構成:①
②存在實數
使得
對任意正整數
都成立.
(1)現在給出只有5項的有限數列
試判斷數列是否為集合的元素；
(2)設數列
的前項和為
且
若對任意正整數
點
均在直線
上，證明:數列
并寫出實數的取值范圍；
(3)設數列
若數列
沒有最大值，求證:數列一定是單調遞增數列。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
和
的項數均為
，則將兩個數列的偏差距離定義為
，其中
.
（1）求數列1，2，7，8和數列2，3，5，6的偏差距離；
（2）設
為滿足遞推關系
的所有數列的集合，和
為中的兩個元素，且項數均為，若
，
，和的偏差距離小于2020，求最大值；
（3）記
是所有7項數列
或
的集合，
，且
中任何兩個元素的偏差距離大于或等于3，證明：中的元素個數小于或等于16.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】曲線
的右焦點分別為
，短袖長為
，點
在曲線
上，
直線
上，且
.
（1）求曲線的標準方程；
（2）試通過計算判斷直線
與曲線公共點的個數.
（3）若點
在都在以線段
為直徑的圓上，且
，試求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】實數a，b滿足ab＞0且a≠b，由a、b、
、
按一定順序構成的數列（ ）
A. 可能是等差數列，也可能是等比數列
B. 可能是等差數列，但不可能是等比數列
C. 不可能是等差數列，但可能是等比數列
D. 不可能是等差數列，也不可能是等比數列
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，空間幾何體由兩部分構成，上部是一個底面半徑為1，高為2的圓錐，下部是一個底面半徑為1，高為2的圓柱，圓錐和圓柱的軸在同一直線上，圓錐的下底面與圓柱的上底面重合，點
是圓錐的頂點，
是圓柱下底面的一條直徑，
、
是圓柱的兩條母線，
是弧的中點.
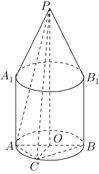
（1）求異面直線
與
所成的角的大小；
（2）求點
到平面
的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
