
【題目】PM2.5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱為可吸入肺顆粒物.我國PM2.5標準采用世衛組織設定的最寬限值,即PM2.5日均值在35微克/立方米以下空氣質量為一級;在35微克/立方米~75微克/立方米之間空氣質量為二級;在75微克/立方米以上空氣質量為超標.
某試點城市環保局從該市市區2015年全年每天的PM2.5監測數據中隨機抽取15天的數據作為樣本,監測值如莖葉圖所示(十位為莖,個位為葉)

(1)求中位數.
(2)從這15天的數據中任取兩天數據,記ξ表示抽到PM2.5監測數據超標的天數,求ξ的分布列及數學期望.
(3)以這15天的PM2.5日均值來估計一年的空氣質量情況,則一年(按360天計算)中平均有多少天的空氣質量達到一級或二級.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
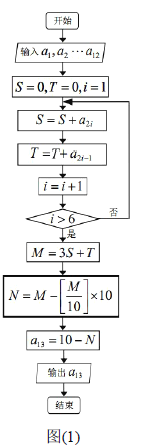
【題目】條形碼是由一組規則排列的條、空及其對應的代碼組成,用來表示一定的信息,我們通常見的條形碼是“![]() ”通用代碼,它是由從左到右排列的
”通用代碼,它是由從左到右排列的![]() 個數字(用
個數字(用![]() ,
,![]() ,…,
,…,![]() 表示)組成,這些數字分別表示前綴部分、制造廠代碼、商品代碼和校驗碼,其中
表示)組成,這些數字分別表示前綴部分、制造廠代碼、商品代碼和校驗碼,其中![]() 是校驗碼,用來校驗前
是校驗碼,用來校驗前![]() 個數字代碼的正確性.圖(1)是計算第
個數字代碼的正確性.圖(1)是計算第![]() 位校驗碼的程序框圖,框圖中符號
位校驗碼的程序框圖,框圖中符號![]() 表示不超過
表示不超過![]() 的最大整數(例如
的最大整數(例如![]() ).現有一條形碼如圖(2)所示(
).現有一條形碼如圖(2)所示(![]() ),其中第
),其中第![]() 個數被污損,那么這個被污損數字
個數被污損,那么這個被污損數字![]() 是( )
是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 作
作![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 于點
于點![]() (點
(點![]() 在
在![]() 軸上方),斜率為
軸上方),斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,且
,且![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)設橢圓![]() 的離心率為
的離心率為![]() ,當點
,當點![]() 為橢圓
為橢圓![]() 的右頂點時,
的右頂點時,![]() 的坐標為
的坐標為 ,求
,求![]() 的值.
的值.
(2)若橢圓![]() 的方程為
的方程為![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠因排污比較嚴重,決定著手整治,一個月時污染度為![]() ,整治后前四個月的污染度如下表:
,整治后前四個月的污染度如下表:
月數 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度為![]() 后,該工廠即停止整治,污染度又開始上升,現用下列三個函數模擬從整治后第一個月開始工廠的污染模式:
后,該工廠即停止整治,污染度又開始上升,現用下列三個函數模擬從整治后第一個月開始工廠的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月數,
表示月數,![]() 、
、![]() 、
、![]() 分別表示污染度.
分別表示污染度.
(1)問選用哪個函數模擬比較合理,并說明理由;
(2)若以比較合理的模擬函數預測,整治后有多少個月的污染度不超過![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2x-4)ex+a(x+2)2(x>0,a∈R,e是自然對數的底數).
(1)若f(x)是(0,+∞)上的單調遞增函數,求實數a的取值范圍;
(2)當a∈![]() 時,證明:函數f(x)有最小值,并求函數f(x)的最小值的取值范圍.
時,證明:函數f(x)有最小值,并求函數f(x)的最小值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,且點
,且點![]() 在橢圓C上.
在橢圓C上.
(1)求橢圓C的標準方程;
(2)過橢圓 上異于其頂點的任意一點Q作圓
上異于其頂點的任意一點Q作圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() 不在坐標軸上),若直線
不在坐標軸上),若直線![]() 在x軸,y軸上的截距分別為
在x軸,y軸上的截距分別為![]() ,證明:
,證明:![]() 為定值;
為定值;
(3)若![]() 是橢圓
是橢圓![]() 上不同兩點,
上不同兩點,![]() 軸,圓E過
軸,圓E過![]() ,且橢圓
,且橢圓![]() 上任意一點都不在圓E內,則稱圓E為該橢圓的一個內切圓,試問:橢圓
上任意一點都不在圓E內,則稱圓E為該橢圓的一個內切圓,試問:橢圓![]() 是否存在過焦點F的內切圓?若存在,求出圓心E的坐標;若不存在,請說明理由.
是否存在過焦點F的內切圓?若存在,求出圓心E的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為定義在實數集
為定義在實數集![]() 上的函數,把方程
上的函數,把方程![]() 稱為函數
稱為函數![]() 的特征方程,特征方程的兩個實根
的特征方程,特征方程的兩個實根![]() 、
、![]() (
(![]() ),稱為
),稱為![]() 的特征根.
的特征根.
(1)討論函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)已知![]() 為給定實數,求
為給定實數,求![]() 的表達式;
的表達式;
(3)把函數![]() ,
,![]() 的最大值記作
的最大值記作![]() ,最小值記作
,最小值記作![]() ,研究函數
,研究函數![]() ,
,![]() 的單調性,令
的單調性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com