
分析 (1)利用三角形內角和公式消去A,結合正弦定理即可求解b的值.
(2)若B=$\frac{π}{3}$,利用正弦定理把a,c表示出來,轉化為函數問題求解△ABC周長的范圍.
解答 解:由$3cosC+ccosB=\frac{3sinA}{sinB}$
可得:$3cosC+ccosB=\frac{3sin(B+C)}{sinB}$
?3sinBcosC+c•sinBcosB=3sin(B+C)
?3sinBcosC+c•sinBcosB=3sinBcosC+3sinCcosB
?c•sinBcosB=3sinCcosB
∵$B≠\frac{π}{2}$,
∴cosB≠0,
∴c•sinB=3sinC.
正弦定理可得:bsinC=3sinC,
∴b=3
(2)由(1)得b=3,B=$\frac{π}{3}$,
∴0<A+C$<\frac{2π}{3}$
正弦定理可得:a=2$\sqrt{3}$sinA,c=2$\sqrt{3}$sinC,
那么:△ABC周長l=3+2$\sqrt{3}$(sinA+sinC)=3$+2\sqrt{3}$[sinA+sin($\frac{2π}{3}$-A)]=3$+2\sqrt{3}$[sinA+sin$\frac{2π}{3}$cosA-sinAcos$\frac{2π}{3}$)]=$3+2\sqrt{3}$[$\frac{3}{2}$sinA+$\frac{\sqrt{3}}{2}$cosA]=$3\sqrt{3}$sinA+3cosA+3=6sin(A+$\frac{π}{6}$)+3,
∵$0<A<\frac{2π}{3}$
∴$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$
sin(A+$\frac{π}{6}$)∈($\frac{1}{2}$,1]
∴△ABC周長的范圍是(6,9]
點評 本題考查了正弦定理和的三角形內角和定理的靈活運用,利用三角函數的有界限求解取值范圍問題.屬于中檔題.


科目:高中數學 來源: 題型:解答題
| 時間t | 50 | 110 | 250 |
| 種植成本Q | 150 | 108 | 150 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD與BC交于點M,設$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.
如圖,在△OAB中,$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD與BC交于點M,設$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
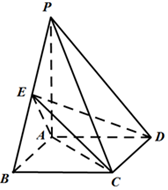 如圖,在四棱錐P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中點.
如圖,在四棱錐P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1] | B. | [-1,0) | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com