
【題目】已知函數![]()
![]() .
.
(1)求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)討論函數![]() 零點的個數.
零點的個數.
【答案】(1)見解析;(2)當![]() 或
或![]() 時,函數有一個零點,當
時,函數有一個零點,當![]() 且
且![]() 時,函數有兩個零點.
時,函數有兩個零點.
【解析】試題分析:
(1)分類討論:當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,![]() ,令
,令![]() 得:
得:![]() ,
,![]() ,則
,則![]() 的單調遞增區間為
的單調遞增區間為![]() .當
.當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,![]() ,當
,當![]() 時,
時,![]() 的單調增區間為
的單調增區間為![]() ,當
,當![]() 時,
時,![]()
![]() .
.![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() .
.
(2)由(1)知當![]() 時,
時,![]() 只有一個零點
只有一個零點![]() ,
,
當![]() 時,
時,![]() 在
在![]() 處取極大值,
處取極大值,![]() 處取極小值.
處取極小值.![]() ,
,![]() ,即
,即![]() 時,函數
時,函數![]() 只有一個零點
只有一個零點![]() ,
,
當![]() 時,令
時,令![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,![]() (當且僅當
(當且僅當![]() 時,等號成立),則:
時,等號成立),則:
![]() 時,
時,![]() 在
在![]() 有兩個零點.
有兩個零點.![]() 時,
時,![]() 在
在![]() 有兩個零點.
有兩個零點.![]() 時,函數在
時,函數在![]() 有一個零點.故當
有一個零點.故當![]() 或
或![]() 時,函數有一個零點,當
時,函數有一個零點,當![]() 且
且![]() 時,函數有兩個零點.
時,函數有兩個零點.
試題解析:
(1)當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,
![]()
![]() ,令
,令![]() 得:
得:
![]() ,
,![]() ,
,
∴![]() 的單調遞增區間為
的單調遞增區間為![]() .
.
當![]() 時,
時,![]() 的定義域為
的定義域為![]() ,
,![]()
![]() ,
,
當![]() 即
即![]() 時,
時,![]() 的單調增區間為
的單調增區間為![]() ,
,
當![]() ,即
,即![]() 時,
時,![]()
![]() .
.
![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() .
.
(2)由(1)知當![]() 時,
時,![]() 在
在![]() 內單調遞增,
內單調遞增,![]() ,
,
故![]() 只有一個零點
只有一個零點![]() ,
,
當![]() 時,
時,![]() 在
在![]() 處取極大值,
處取極大值,![]() 處取極小值.
處取極小值.
由![]() 知
知![]() ,而
,而![]() ,則
,則![]() ,
,
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴當![]() 時,函數
時,函數![]() 只有一個零點
只有一個零點![]() ,
,
當![]() 時,
時,
令![]() ,
,
![]() ,
,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
![]() ,∴
,∴![]() (當且僅當
(當且僅當![]() 時,等號成立),
時,等號成立),
i)![]() 時,
時,
![]() ,
,![]() ,
,![]() ,
,
由(1)函數單調性知,![]() ,所以函數在
,所以函數在![]() 存在零點,
存在零點,
∴![]() 在
在![]() 有兩個零點.
有兩個零點.
ii)![]() 時,
時,
![]() ,
,![]() ,
,![]() ,
,
同理可得函數在![]() 存在零點,
存在零點,
∴![]() 在
在![]() 有兩個零點.
有兩個零點.
iii)![]() 時,
時,
![]() ,函數在
,函數在![]() 有一個零點.
有一個零點.
綜上所述:
當![]() 或
或![]() 時,函數有一個零點,
時,函數有一個零點,
當![]() 且
且![]() 時,函數有兩個零點.
時,函數有兩個零點.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】最近,“百萬英雄”,“沖頂大會”等一些闖關答題類游戲風靡全國,既能答題,又能學知識,還能掙獎金。若某闖關答題一輪共有4類題型,選手從前往后逐類回答,若中途回答錯誤,立馬淘汰只能觀戰;若能堅持到4類題型全部回答正確,就能分得現金并獲得一枚復活幣。每一輪闖關答題順序為:1.文史常識類;2.數理常識類;3.生活常識類;4.影視藝術常識類,現從全省高中生中調查了100位同學的答題情況統計如下表:

(Ⅰ)現用樣本的數據特征估算整體的數據特征,從全省高中生挑選4位同學,記![]() 為4位同學獲得獎金的總人數,求
為4位同學獲得獎金的總人數,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若王同學某輪闖關獲得的復活幣,系統會在下一輪游戲中自動使用,即下一輪重新進行闖關答題時,若王同學在某一類題型中回答錯誤,自動復活一次,視為答對該類題型。請問:仍用樣本的數據特征估算王同學的數據特征,那么王同學在獲得復活幣的下一輪答題游戲中能夠最終獲得獎金的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的下頂點為
的下頂點為![]() ,右頂點為
,右頂點為![]() ,離心率
,離心率![]() ,拋物線
,拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 是拋物線
是拋物線![]() 上一點,拋物線
上一點,拋物線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,且
,且![]() .
.
(1)求直線![]() 的方程;
的方程;
(2)若![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求
,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
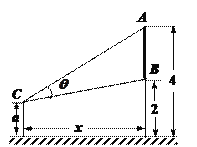
【題目】如圖,墻上有一壁畫,最高點![]() 離地面4米,最低點
離地面4米,最低點![]() 離地面2米,觀察者從距離墻
離地面2米,觀察者從距離墻![]() 米,離地面高
米,離地面高![]() 米的
米的![]() 處觀賞該壁畫,設觀賞視角
處觀賞該壁畫,設觀賞視角![]()
(1)若![]() 問:觀察者離墻多遠時,視角
問:觀察者離墻多遠時,視角![]() 最大?
最大?
(2)若![]() 當
當![]() 變化時,求
變化時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
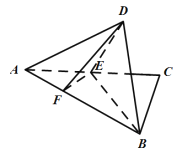
【題目】直角三角形![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() 是線段
是線段![]() 上一個動點,且
上一個動點,且![]() ,如圖所示,沿
,如圖所示,沿![]() 將
將![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
(1)當![]() 時,證明:
時,證明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 與平面
與平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 上的任一點到焦點的距離最大值為3,離心率為
上的任一點到焦點的距離最大值為3,離心率為![]() ,
,
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為曲線
為曲線![]() 上兩點,
上兩點, ![]() 為坐標原點,直線
為坐標原點,直線![]() 的斜率分別為
的斜率分別為![]() ,且
,且![]() ,求直線
,求直線![]() 被圓
被圓![]() 截得弦長的最大值及此時直線
截得弦長的最大值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com