
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
分析 化簡三角函數(shù),然后判斷三個數(shù)的大小.
解答 解:a=cos127°cos50°+sin53°cos40°
=-sin53°(sin40°+cos40°)=$\sqrt{2}$sin53°sin85°$>\sqrt{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$$>\frac{\sqrt{3}}{2}$,
b=$\frac{\sqrt{2}}{2}$(sin56°-cos56°)=sin11°∈(0,$\frac{1}{2}$),
c=$\frac{1}{2}$(cos80°-2cos250°+1)=$\frac{1}{2}$(cos80°-cos100°)=sin10°,
sin11°>sin10°.
所以a>b>c.
故選:A.
點(diǎn)評 本題考查三角函數(shù)的化簡求值,正弦函數(shù)的單調(diào)性,兩角和與差的三角函數(shù),考查計(jì)算能力.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
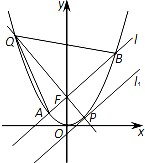 如圖,過拋物線C:x2=2py(p>0)的焦點(diǎn)F作直線l與拋物線相交于A,B兩點(diǎn).直線l1∥l,且與拋物線C相切于點(diǎn)P,直線PF交拋物線于另一點(diǎn)Q.已知拋物線C上縱坐標(biāo)為$\frac{3p}{2}$的點(diǎn)M到焦點(diǎn)F的距離為2.
如圖,過拋物線C:x2=2py(p>0)的焦點(diǎn)F作直線l與拋物線相交于A,B兩點(diǎn).直線l1∥l,且與拋物線C相切于點(diǎn)P,直線PF交拋物線于另一點(diǎn)Q.已知拋物線C上縱坐標(biāo)為$\frac{3p}{2}$的點(diǎn)M到焦點(diǎn)F的距離為2.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
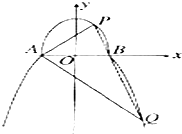 如圖,曲線C由上半橢圓C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分拋物線C2:y=-x2+1(y≤0)連接而成,C1、C2的公共點(diǎn)為A,B,其中C1的離心率為$\frac{\sqrt{3}}{2}$.
如圖,曲線C由上半橢圓C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分拋物線C2:y=-x2+1(y≤0)連接而成,C1、C2的公共點(diǎn)為A,B,其中C1的離心率為$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com