
 如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中點.
如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中點.分析 (1)取PA的中點F,連接EF,BF,通過證明CE∥BF,利用直線與平面平行的判定定理證明即可.
(2)利用已知條件轉化求解M到底面的距離,作出二面角的平面角,然后求解二面角M-AB-D的余弦值即可.
解答 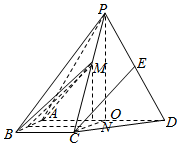
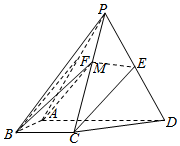 (1)證明:取PA的中點F,連接EF,BF,因為E是PD的中點,
(1)證明:取PA的中點F,連接EF,BF,因為E是PD的中點,
所以EF$\underset{∥}{=}$$\frac{1}{2}$AD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,∴BC∥$\frac{1}{2}$AD,
∴BCEF是平行四邊形,可得CE∥BF,BF?平面PAB,CE?平面PAB,
∴直線CE∥平面PAB;
(2)解:四棱錐P-ABCD中,
側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,
∠BAD=∠ABC=90°,E是PD的中點.
取AD的中點O,M在底面ABCD上的射影N在OC上,設AD=2,則AB=BC=1,OP=$\sqrt{3}$,
∴∠PCO=60°,直線BM與底面ABCD所成角為45°,
可得:BN=MN,CN=$\frac{\sqrt{3}}{3}$MN,BC=1,
可得:1+$\frac{1}{3}$BN2=BN2,BN=$\frac{\sqrt{6}}{2}$,MN=$\frac{\sqrt{6}}{2}$,
作NQ⊥AB于Q,連接MQ,
所以∠MQN就是二面角M-AB-D的平面角,MQ=$\sqrt{{1}^{2}+(\frac{\sqrt{6}}{2})^{2}}$
=$\frac{\sqrt{10}}{2}$,
二面角M-AB-D的余弦值為:$\frac{1}{\frac{\sqrt{10}}{2}}$=$\frac{\sqrt{10}}{5}$.
點評 本題考查直線與平面平行的判定定理的應用,二面角的平面角的求法,考查空間想象能力以及計算能力.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
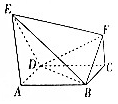 如圖,正方形ABCD的邊長為1,E,F是平面ABCD同一側的兩點,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如圖,正方形ABCD的邊長為1,E,F是平面ABCD同一側的兩點,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
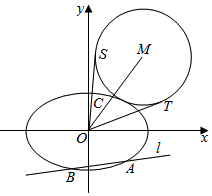 在平面直角坐標系xOy中,橢圓E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,焦距為2.
在平面直角坐標系xOy中,橢圓E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,焦距為2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com