
| A. | [1,1+$\sqrt{2}$] | B. | [2-$\sqrt{2}$,2+$\sqrt{2}$] | C. | [$\sqrt{2},2\sqrt{2}$] | D. | [3-2$\sqrt{2}$,3+2$\sqrt{2}$] |
分析 由$\overrightarrow{a}$,$\overrightarrow{b}$是單位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0.可設$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y).由向量$\overrightarrow{c}$滿足|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=2,可得(x-1)2+(y-1)2=4.其圓心C(1,1),半徑r=2.利用|OC|-r≤|$\overrightarrow{c}$|=$\sqrt{{x}^{2}{+y}^{2}}$≤|OC|+r即可得出.
解答 解:由$\overrightarrow{a}$,$\overrightarrow{b}$是單位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,
可設$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y),
由向量$\overrightarrow{c}$滿足|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
∴|(x-1,y-1)|=2,
∴$\sqrt{{(x-1)}^{2}{+(y-1)}^{2}}$=2,即(x-1)2+(y-1)2=4,
其圓心C(1,1),半徑r=2,
∴|OC|=$\sqrt{2}$
∴2-$\sqrt{2}$≤|$\overrightarrow{c}$|=$\sqrt{{x}^{2}{+y}^{2}}$≤2+$\sqrt{2}$.
故選:B.
點評 本題考查了向量的垂直與數量積的關系、數量積的運算性質、點與圓上的點的距離大小關系,考查了推理能力和計算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
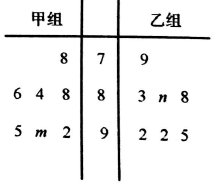 某中學奧數培訓班共有14人,分為兩個小組,在一次階段測試中兩個小組成績的莖葉圖如圖所示,其中甲組學生成績的平均數是88,乙組學生成績的中位數是89,則n-m的值( )
某中學奧數培訓班共有14人,分為兩個小組,在一次階段測試中兩個小組成績的莖葉圖如圖所示,其中甲組學生成績的平均數是88,乙組學生成績的中位數是89,則n-m的值( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0$<\frac{r}{L}<\frac{1}{2}$ | B. | $\frac{1}{2}≤\frac{r}{L}<1$ | C. | 0$<\frac{r}{L}<\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}≤\frac{r}{L}<1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com