日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
7．已知函數f（x）=ax3+bx+7（其中a，b為常數），若f（-7）=-17，則f（7）的值為（　　）
A．31B．17C．-17D．15

分析 直接利用函數的奇偶性的性質轉化求解即可．

解答 解：函數f（x）=ax3+bx+7（其中a，b為常數），若f（-7）=-a•73-7b+7=-17，
則f（7）=a•73+7b+7=-（-a•73-7b+7）+14=17+14=31．
故選：A．

點評 本題考查函數的奇偶性的性質的應用，考查計算能力．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：選擇題

17．直線xsin 30°+ycos 150°+1=0的斜率是（　　）
A．$\frac{\sqrt{3}}{3}$B．$\sqrt{3}$C．-$\sqrt{3}$D．-$\frac{\sqrt{3}}{3}$

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

18．已知$\overrightarrow{a}$=（3，4），$\overrightarrow{b}$=（2，1），則$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影為（　　）
A．2B．5$\sqrt{2}$C．2$\sqrt{5}$D．5

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

15．拋物線y2=12x上與焦點的距離等于6的點的坐標是（3，6）或（3，-6）．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

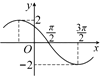2．已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，φ∈（0，π）），其導函數f'（x）的部分圖象如圖所示，則下列對f（x）的說法正確的是（　　）
A．最大值為4且關于直線$x=-\frac{π}{2}$對稱
B．最大值為4且在$[{-\frac{π}{2}\;\;，\;\;\frac{π}{2}}]$上單調遞增
C．最大值為2且關于點$（{-\frac{π}{2}\;\;，\;\;0}）$中心對稱
D．最大值為2且在$[{-\frac{π}{2}\;\;，\;\;\frac{3π}{2}}]$上單調遞減

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

12．記F（x，y）=x+y-a（2$\sqrt{3xy}$+x），存在x0∈R+使F（x0，3）=3，則實數a滿足（　　）
A．0＜a＜1B．0≤a＜1C．0＜a≤1D．0＜a≤1

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

19．在等差數列{an}中，首項a1=-20，公差d=3，則|a1|+|a2|+|a3|+…+|a11|=（　　）
A．99B．100C．-55D．98

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

16．已知約束條件$\left\{\begin{array}{l}x≥k\\ x+y-4≤0\\ x-y≤0\end{array}\right.$表示面積為1的直角三角形區域，則實數k的值為（　　）
A．0B．1C．1或3D．3

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

17．已知f（x）=$\left\{\begin{array}{l}{x-5（x≥6）}\\{f（x+2）（x＜6）}\end{array}\right.$，則f（1）為（　　）
A．2B．3C．4D．5

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 欧美一级在线观看视频 | 久久88 | 午夜午夜精品一区二区三区文 | 国产91极品 | 91麻豆精品一区二区三区 | 午夜欧美一区二区三区在线播放 | 欧美二区在线 | 日韩h在线观看 | 亚洲精品视频免费 | 久久精品国产99 | 国产污视频网站 | 精品中文字幕在线观看 | 黄色大片在线播放 | 欧美在线观看免费观看视频 | 国产精品久久久99 | 久久久xxxx | 一区二区中文字幕 | 欧美激情一区二区三区四区 | 久草日韩 | 亚洲综合在线播放 | 婷婷色站 | av超碰| 国产精品久久久久久久久免费 | 毛片在线视频 | 欧美日韩中文在线观看 | 成人福利视频 | 噜噜噜天天躁狠狠躁夜夜精品 | 国产一区亚洲 | 91久久久久| 成人免费在线视频 | 欧美一区二区三 | 国产精品久久久久久福利一牛影视 | 岛国伊人| 九色影院 | 国产精品久久久久久久久久久久久久久久久 | 福利精品视频 | 国产精品久久久久久久久久99 | 99精品亚洲国产精品久久不卡 | 亚洲视频免费在线观看 | 国产aⅴ爽av久久久久 | 国产精品27页 |