
分析 設f(x)=λ,研究f(x)的單調性和極值,得出f(x)=λ的解的情況,從而確定關于λ的方程λ2-tλ+1=0的解的分布情況,利用二次函數的性質得出t的范圍.
解答 解:f(x)=$\left\{\begin{array}{l}{x{e}^{x},x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,
當x≥0時,f′(x)=ex+xex=(1+x)ex>0,
∴f(x)在[0,+∞)上是增函數,
當x<0時,f′(x)=-ex-xex=(-1-x)ex,
∴當x<-1時,f′(x)>0,當-1<x<0時,f′(x)<0,
∴f(x)在(-∞,-1]上是增函數,在(-1,0)上是減函數.
當x=-1時,f(x)取得極大值f(-1)=$\frac{1}{e}$.
令f(x)=λ,
又f(x)≥0,f(0)=0,
則當λ<0時,方程f(x)=λ無解;
當λ=0或λ>$\frac{1}{e}$時,方程f(x)=λ有一解;
當λ=$\frac{1}{e}$時,方程f(x)=λ有兩解;
當0<λ<$\frac{1}{e}$時,方程f(x)=λ有三解.
∵g(x)=f2(x)-tf(x)=-1有四個不同的實數解,
∴關于λ的方程λ2-tλ+1=0在(0,$\frac{1}{e}$)和($\frac{1}{e}$,+∞)上各有一解,
∴$\left\{\begin{array}{l}{{t}^{2}-4>0}\\{\frac{1}{{e}^{2}}-\frac{t}{e}+1<0}\end{array}\right.$,解得t$>e+\frac{1}{e}$.
故答案為(e+$\frac{1}{e}$,+∞).
點評 本題考查了函數的零點個數與單調性和極值的關系,二次函數的性質,換元法解題思想,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)在$(0,\frac{π}{4})$上單調遞減 | B. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上單調遞減 | ||
| C. | f(x)在$(0,\frac{π}{4})$上單調遞增 | D. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上單調遞增 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
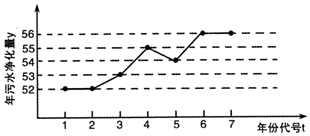
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
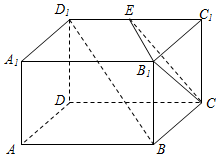 已知長方體AC1中,AD=AB=2,AA1=1,E為D1C1的中點,如圖所示.
已知長方體AC1中,AD=AB=2,AA1=1,E為D1C1的中點,如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 如果m∥n,α∥β,那么m與α所成的角和n與β所成的角相等 | |
| B. | 如果m⊥n,m⊥α,n∥β,那么α⊥β | |
| C. | 如果α∥β,m?α,那么m∥β | |
| D. | 如果m⊥α,n∥α,那么m⊥n |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
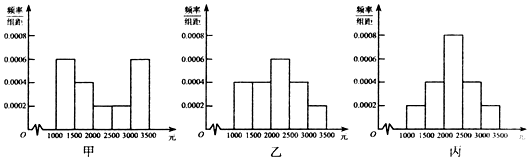
| A. | s1>s2>s3 | B. | s1>s3>s2 | C. | s3>s2>s1 | D. | s3>s1>s2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com