
 將石子擺成如圖所示的梯形形狀,稱數列5,9,14,20,…為“梯形數”.根據圖形的構成,此數列的第100項,即a100=5252.
將石子擺成如圖所示的梯形形狀,稱數列5,9,14,20,…為“梯形數”.根據圖形的構成,此數列的第100項,即a100=5252. 分析 根據題意,分析所給的圖形可得an-an-1=n+2(n≥2),結合a1的值,可得a100=a1+(a2-a1)+(a3-a2)+…+(a100-a99),代入數據計算可得答案.
解答 解:根據題意,分析相鄰兩個圖形的點數之間的關系:
a2-a1=4,
a3-a2=5,
…
由此我們可以推斷:an-an-1=n+2(n≥2),
又由a1=5,
所以a100=a1+(a2-a1)+(a3-a2)+…+(a100-a99)=5+4+5+…+102=5+$\frac{99×(4+102)}{2}$=5252;
即a100=5252;
故答案為:5252.
點評 本題考查數列的表示方法,涉及歸納推理的運用,關鍵是依據圖形,發現變化的規律.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
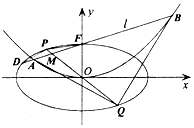 在平面直角坐標系xOy中,拋物線E:x2=4y的焦點F是橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一個頂點.過點F且斜率為k(k≠0)的直線l交橢圓C于另一點D,交拋物線E于A、B兩點,線段DF的中點為M,直線OM交橢圓C于P、Q兩點,記直線OM的斜率為k',滿足$k•k'=-\frac{1}{4}$.
在平面直角坐標系xOy中,拋物線E:x2=4y的焦點F是橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一個頂點.過點F且斜率為k(k≠0)的直線l交橢圓C于另一點D,交拋物線E于A、B兩點,線段DF的中點為M,直線OM交橢圓C于P、Q兩點,記直線OM的斜率為k',滿足$k•k'=-\frac{1}{4}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18歲至31歲 | 8 | 12 | 20 | 60 | 140 | 150 |
| 32歲至44歲 | 12 | 28 | 20 | 140 | 60 | 150 |
| 45歲至59歲 | 25 | 50 | 80 | 100 | 225 | 450 |
| 60歲及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
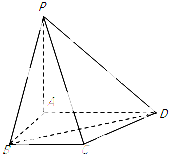 如圖,四棱錐P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.
如圖,四棱錐P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com