
以下四個關于圓錐曲線的命題中:
①設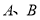 為兩個定點,
為兩個定點,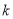 為非零常數,
為非零常數, ,則動點
,則動點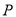 的軌跡為雙曲線;
的軌跡為雙曲線;
②過定圓 上一定點
上一定點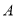 作圓的動點弦
作圓的動點弦 ,
,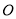 為坐標原點,若
為坐標原點,若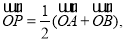 則動點
則動點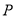 的軌跡為圓;
的軌跡為圓;
③ ,則雙曲線
,則雙曲線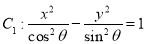 與
與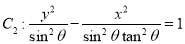 的離心率相同;
的離心率相同;
④已知兩定點 和一動點
和一動點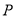 ,若
,若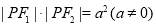 ,則點
,則點 的軌跡關于原點對稱.
的軌跡關于原點對稱.
其中真命題的序號為 (寫出所有真命題的序號).
②③④
【解析】
試題分析:①錯誤.若動點 的軌跡為雙曲線,則
的軌跡為雙曲線,則 要小于
要小于 兩個定點間的距離,當
兩個定點間的距離,當 大于
大于 兩個定點間的距離時動點
兩個定點間的距離時動點 的軌跡無圖形,當
的軌跡無圖形,當 等于
等于 兩個定點間的距離時,動點
兩個定點間的距離時,動點 的軌跡是兩條射線;
的軌跡是兩條射線;
②正確.根據平面向量加法的平行四邊形法則,易知點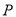 是
是 的中點.根據垂徑定理,圓心與弦的中點連線垂直于這條弦,在定圓
的中點.根據垂徑定理,圓心與弦的中點連線垂直于這條弦,在定圓 上,有
上,有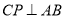 ,即
,即 恒為直角.由于
恒為直角.由于 是圓的半徑,是一個定長,且
是圓的半徑,是一個定長,且 ,所以點
,所以點 在以
在以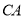 為直徑的圓上運動,所以動點
為直徑的圓上運動,所以動點 的軌跡是一個圓.
的軌跡是一個圓.
③正確.雙曲線 的離心率,由:
的離心率,由: 且
且 ,解得
,解得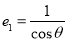 ;
;
雙曲線 的離心率,由
的離心率,由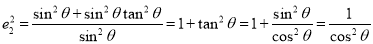 ,又因為
,又因為 ,所以
,所以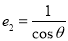 ,綜上,
,綜上, 所以兩個雙曲線的離心率相同,正確.
所以兩個雙曲線的離心率相同,正確.
④正確.設 ,所以
,所以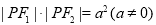 即:
即: ,設
,設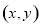 為曲線
為曲線 上任意一點,則點
上任意一點,則點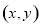 關于原點的對稱點
關于原點的對稱點 ,因為
,因為
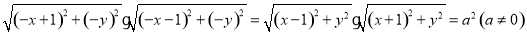 ,即點
,即點 也在曲線
也在曲線 上,所以命題正確.
上,所以命題正確.
綜上正確命題的序號是②③④.
考點:1.雙曲線的定義;2.動點的軌跡;3.雙曲線的離心率.


科目:高中數學 來源: 題型:單選題
對于函數f(x),如果存在銳角θ使得f(x)的圖象繞坐標原點逆時針旋轉角θ,所得曲線仍是一函數,則稱函數f(x)具備角θ的旋轉性,下列函數具有角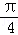 的旋轉性的是( )
的旋轉性的是( )
A.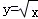 | B.y=lnx | C.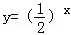 | D.y=x2 |
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江西省贛州市北校高二1月月考理科數學試卷(解析版) 題型:解答題
.已知圓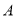 :x2+y2-2x-2y-2=0.
:x2+y2-2x-2y-2=0.
(1)若直線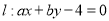 平分圓
平分圓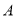 的周長,求原點O到直線
的周長,求原點O到直線 的距離的最大值;
的距離的最大值;
(2)若圓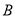 平分圓
平分圓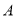 的周長,圓心
的周長,圓心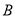 在直線y=2x上,求符合條件且半徑最小的圓B的方程.
在直線y=2x上,求符合條件且半徑最小的圓B的方程.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江西省贛州市北校高二1月月考理科數學試卷(解析版) 題型:選擇題
如圖,正方體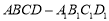 的棱長為
的棱長為 ,點
,點 在棱
在棱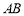 上,且
上,且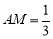 ,點
,點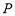 是平面
是平面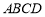 上的動點,且動點
上的動點,且動點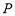 到直線
到直線 的距離與點
的距離與點 到點
到點 的距離的平方差為
的距離的平方差為 ,則動點
,則動點 的軌跡是 ( )
的軌跡是 ( )

A.圓 B.拋物線 C.雙曲線 D.橢圓
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江西省贛州市北校高二1月月考理科數學試卷(解析版) 題型:選擇題
如圖是某賽季甲、乙兩名籃球運動員每場比賽得分的莖葉圖,則甲、乙兩人這幾場比賽得分的中位數之和是( )
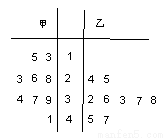
A.62 B.63 C.64 D.56
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com