
分析 逐項分析.①根據一次函數的單調性易得;②根據反比例函數的圖象和性質易知其值域應為(0,$\frac{1}{2}$);③可舉反例說明;④利用均值不等式可得.
解答 解:①當x≤0時,2x+1≤1,故①正確;
②由反比例函數的圖象和性質知,當x>2時,$0<\frac{1}{x}<\frac{1}{2}$,故②錯誤;
③當函數定義域為[0,2]時,函數值域也為[0,4],故③錯誤;
④當x<0時,$y=x+\frac{1}{x}=-[(-x)+\frac{1}{-x}]$.因為$(-x)+\frac{1}{-x}≥2\sqrt{(-x)•\frac{1}{-x}}=2$,所以y≤-2,故④正確.
綜上可知:②③錯誤.
故答案為:②③.
點評 本題考查函數的概念和性質.利用函數性質和圖象是解題關鍵.其中命題④的判斷是本題易錯點.屬于中檔題.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:選擇題
| A. | {y|$\frac{1}{2}$<y<1} | B. | {y|0<y$<\frac{1}{2}$} | C. | ∅ | D. | {y|0<y<1} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 明天上午下雨,下午不下雨 | |
| B. | 明天下雨的概率為80% | |
| C. | 明天有的地方下雨,有的地方不下雨 | |
| D. | 明天下雨的時間一共是19.2小時 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
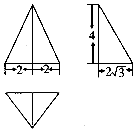
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com