
| A. | 9 | B. | 8 | C. | 18 | D. | 16 |
分析 如圖所示,△ABC滿足$\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3},∠BAC={30°}$,可得cbcos30°=2$\sqrt{3}$,解得bc=4.可得S△ABC=$\frac{1}{2}$bcsin30°=1,可得x+y=$\frac{1}{2}$.(x,y>0).再利用“乘1法”與基本不等式的性質即可得出.
解答 解:如圖所示,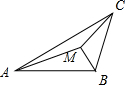
∵△ABC滿足$\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3},∠BAC={30°}$,
∴cbcos30°=2$\sqrt{3}$,解得bc=4.
∴S△ABC=$\frac{1}{2}$bcsin30°=$\frac{1}{2}×4×\frac{1}{2}$=1,
∴x+y+$\frac{1}{2}$=1,解得x+y=$\frac{1}{2}$.(x,y>0).
∴$\frac{1}{x}+\frac{4}{y}$=2(x+y)$(\frac{1}{x}+\frac{4}{y})$=$2(5+\frac{y}{x}+\frac{4x}{y})$≥$2(5+2\sqrt{\frac{y}{x}•\frac{4x}{y}})$=18,當且僅當y=2x=$\frac{1}{3}$時取等號.
故選:C.
點評 本題考查了數量積運算性質、“乘1法”與基本不等式的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 命題“?x∈R.ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命題“若a=-1,則函數f(x)=ax2+2x-1只有一個零點”的逆命題是真命題 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“對于x∈[1,2]有(x2+2x)min≥(ax)max” | |
| D. | 命題“已知x,y∈R,若x+y≠3,則x≠2或y≠1”是真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一、三象限角 | B. | 第二、四象限角 | C. | 第二、三象限角 | D. | 第一、四象限角 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
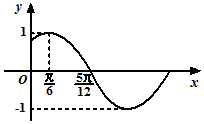 已知函數$f(x)=Msin(ωx+φ)(M>0,|φ|<\frac{π}{2})$的部分圖象如圖所示.
已知函數$f(x)=Msin(ωx+φ)(M>0,|φ|<\frac{π}{2})$的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 經過不同的三點有且只有一個平面 | |
| B. | 沒有公共點的兩條直線一定平行 | |
| C. | 垂直于同一平面的兩直線是平行直線 | |
| D. | 垂直于同一平面的兩平面是平行平面 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com