
| A. | 4 | B. | 6 | C. | $4-2\sqrt{5}$ | D. | $2\sqrt{5}+2$ |
分析 確定函數F(a,b)=$\frac{1}{2}$(a+b-|a-b|)的含義,表示出G(x)=F(f(x),g(x)),根據一次函數與二次函數的性質可求函數的最大值.
解答 解:∵F(a,b)=$\frac{1}{2}$(a+b-|a-b|)=$\left\{\begin{array}{l}{b,a≥b}\\{a,a<b}\end{array}\right.$,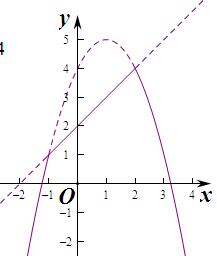
∴設G(x)=F(f(x),g(x))=$\left\{\begin{array}{l}{g(x),f(x)≥g(x)}\\{f(x),f(x)<g(x)}\end{array}\right.$.
∵當-1≤x≤2時,f(x)≥g(x),此時G(x)=x+2∈[1,4],
此時函數無零點,此時最大值為4,
當x>2或x<-1時,f(x)<g(x),G(x)=-x2+2x+4=-(x-1)2+3<4,
綜上可得,函數G(x)的最大值為4,
由G(x)=-x2+2x+4=0,得方程的兩根之和為2,
則函數F(f(x),g(x))的最大值與零點之和為2+4=6,
故選:B.
點評 本題主要考查分段函數的應用,以及函數的最值的求解,解題的關鍵是根據題目中的定義求出函數G(x)的解析式.利用數形結合是解決本題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
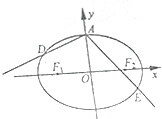 如圖,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,長軸長為2$\sqrt{2}$,左、右焦點分別為F1,F2,上頂點為A.
如圖,橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,長軸長為2$\sqrt{2}$,左、右焦點分別為F1,F2,上頂點為A.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8π | B. | 24π | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a3<b3 | B. | a3>b3 | C. | a6<b6 | D. | a6>b6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 關于直線x=$\frac{π}{12}$對稱 | B. | 關于直線x=$\frac{5π}{12}$對稱 | ||
| C. | 關于點($\frac{π}{12}$,0)對稱 | D. | 關于點($\frac{5π}{12}$,0)對稱 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com