
分析 先求函數的定義域,根據復合函數的單調性“同增異減”求解.
解答 解:由題意:函數f(x)=$\sqrt{{x}^{2}-2}$的定義域為{x|$x≥\sqrt{2}$或x$≤-\sqrt{2}$},
令x2-2=t,則函數f(x)=$\sqrt{{x}^{2}-2}$轉化為g(t)=${t}^{\frac{1}{2}}$,(t≥0)在其定義域內為增函數.
函數t=x2-2根據二次函數的圖象及性質可知:
當x在$[\sqrt{2}$,+∞)時,函數t為單調增函數,當x在$(-∞,-\sqrt{2}]$時,函數t為單調減函數,
根據復合函數的單調性“同增異減”,
∴函數f(x)=$\sqrt{{x}^{2}-2}$的單調增區間是$[\sqrt{2}$,+∞).
故答案為:$[\sqrt{2}$,+∞).
點評 本題考查了復合函數的單調性問題,要抓住定義域的范圍和復合函數的單調性“同增異減”來求解.屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | 2016+ln8 | B. | 4032+ln4 | C. | 2016+21n2 | D. | 4032+ln2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
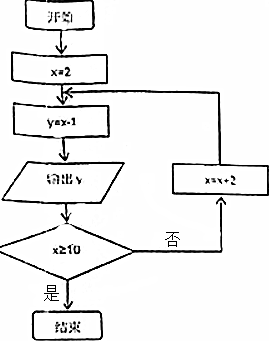 在如圖所示的程序框圖中,記所有的x的值組成的集合為A,由輸出的數據y組成的集合為B.
在如圖所示的程序框圖中,記所有的x的值組成的集合為A,由輸出的數據y組成的集合為B.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com