
【題目】已知函數![]() 有三個不同的零點
有三個不同的零點![]() ,
, ![]() ,
, ![]() (其中
(其中![]() ),則
),則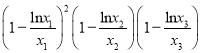 的值為( )
的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】令f(x)=0,分離變量可得a=![]() ,
,
令g(x)=![]() ,
,
由g′(x)= =0,得x=1或x=e.
=0,得x=1或x=e.
當x∈(0,1)時,g′(x)<0;當x∈(1,e)時,g′(x)>0;當x∈(e,+∞)時,g′(x)<0.
即g(x)在(0,1),(e,+∞)上為減函數,在(1,e)上為增函數.
∴0<x1<1<x2<e<x3,
a=![]() =
= ,令μ=
,令μ=![]() ,
,
則a=![]() ﹣μ,即μ2+(a﹣1)μ+1﹣a=0,
﹣μ,即μ2+(a﹣1)μ+1﹣a=0,
μ1+μ2=1﹣a<0,μ1μ2=1﹣a<0,
對于μ=![]() ,μ′=
,μ′=![]()
則當0<x<e時,μ′>0;當x>e時,μ′<0.而當x>e時,μ恒大于0.
畫其簡圖,

不妨設μ1<μ2,則μ1=![]() ,μ2=
,μ2=![]() =
=![]() =μ3,
=μ3,
∴(1﹣![]() )2(1﹣
)2(1﹣![]() )(1﹣
)(1﹣![]() )=(1﹣μ1)2(1﹣μ2)(1﹣μ3)
)=(1﹣μ1)2(1﹣μ2)(1﹣μ3)
=[(1﹣μ1)(1﹣μ2)]2=[1﹣(1﹣a)+(1﹣a)]2=1.
故選:D.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,A是△BCD所在平面外一點,M、N為△ABC和△ACD重心,BD=6; 
(1)求MN的長;
(2)若A、C的位置發生變化,MN的位置和長度會改變嗎?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某餐廳裝修,需要大塊膠合板![]() 張,小塊膠合板
張,小塊膠合板![]() 張,已知市場出售
張,已知市場出售![]() 兩種不同規格的膠合板。經過測算,
兩種不同規格的膠合板。經過測算, ![]() 種規格的膠合板可同時截得大塊膠合板
種規格的膠合板可同時截得大塊膠合板![]() 張,小塊膠合板
張,小塊膠合板![]() 張,
張, ![]() 種規格的膠合板可同時截得大塊膠合板
種規格的膠合板可同時截得大塊膠合板![]() 張,小塊膠合板
張,小塊膠合板![]() 張.已知
張.已知![]() 種規格膠合板每張
種規格膠合板每張![]() 元,
元, ![]() 種規格膠合板每張
種規格膠合板每張![]() 元.分別用
元.分別用![]() 表示購買
表示購買![]() 兩種不同規格的膠合板的張數.
兩種不同規格的膠合板的張數.
(1)用![]() 列出滿足條件的數學關系式,并畫出相應的平面區域;
列出滿足條件的數學關系式,并畫出相應的平面區域;
(2)根據施工需求, ![]() 兩種不同規格的膠合板各買多少張花費資金最少?并求出最少資金數.
兩種不同規格的膠合板各買多少張花費資金最少?并求出最少資金數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一張紙沿直線l對折一次后,點A(0,4)與點B(8,0)重疊,點C(6,8)與點D(m,n)重疊.
(1)求直線l的方程;
(2)求m+n的值;
(3)直線l上是否存在一點P,使得||PB|﹣|PC||存在最大值,如果存在,請求出最大值,以及此時點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=2sin(2x+ ![]() )的圖象向右平移φ(φ>0)個單位,再將圖象上每一點橫坐標縮短到原來的
)的圖象向右平移φ(φ>0)個單位,再將圖象上每一點橫坐標縮短到原來的 ![]() 倍,所得圖象關于直線x=
倍,所得圖象關于直線x= ![]() 對稱,則φ的最小正值為 .
對稱,則φ的最小正值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)的定義域為D,若存在非零實數m,使得對于任意x∈M(MD),有(x﹣m)∈D且f(x﹣m)≤f(x),則稱f(x)為M上的m度低調函數.如果定義域為R的函數f(x)是奇函數,當x≥0時,f(x)=|x﹣a2|﹣a2 , 且f(x)為R上的5度低調函數,那么實數a的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確的序號是 . ①y=﹣2cos( ![]() π﹣2x)是奇函數;
π﹣2x)是奇函數;
②若α,β是第一象限角,且α>β,則sinα>sinβ;
③x=﹣ ![]() 是函數y=3sin(2x﹣
是函數y=3sin(2x﹣ ![]() )的一條對稱軸;
)的一條對稱軸;
④函數y=sin( ![]() ﹣2x)的單調減區間是[kπ﹣
﹣2x)的單調減區間是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心為C的圓過點A(0,﹣6)和B(1,﹣5),且圓心在直線l:x﹣y+1=0上.
(1)求圓心為C的圓的標準方程;
(2)過點M(2,8)作圓的切線,求切線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com