
【題目】設函數![]()
(1)若![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() ,求
,求![]() 的值;
的值;
(2)求函數![]() 的單調區間;
的單調區間;
(3)若![]() ,求證:在
,求證:在![]() 時,
時, ![]() .
.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時, ![]() 的單調減區間為
的單調減區間為![]() .單調增區間為
.單調增區間為![]() ;
;
當![]() 時,
時, ![]() 的單調減區間為
的單調減區間為![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】試題分析:(1)先求出![]() ,通過
,通過![]() 在點
在點![]() 處的切線斜率,可得
處的切線斜率,可得![]() ,解得
,解得![]() ;(2)由(1)知:
;(2)由(1)知: ![]() ,結合導數分①
,結合導數分①![]() 、②
、②![]() 兩種情況討論分別令
兩種情況討論分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;;(3)通過變形,只需證明
的減區間;;(3)通過變形,只需證明![]() 即可,利用
即可,利用![]() ,根據指數函數及冪函數的性質、函數的單調性及零點判定定理即得到結論.
,根據指數函數及冪函數的性質、函數的單調性及零點判定定理即得到結論.
試題解析:(1)若![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() ,
,
![]() ,
,
得![]() .
.
(2)由![]()
當![]() 時,令
時,令![]() 解得:
解得: ![]()
當![]() 變化時,
變化時, ![]() 隨
隨![]() 變化情況如表:
變化情況如表:
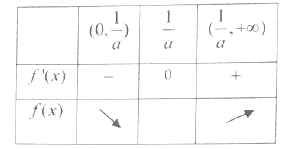
由表可知: ![]() 在
在![]() 上是單調減函數,在
上是單調減函數,在![]() 上是單調增函數
上是單調增函數
當![]() 時,
時, ![]() ,
, ![]() 的單調減區間為
的單調減區間為![]()
所以,當![]() 時,
時, ![]() 的單調減區間為
的單調減區間為![]() .單調增區間為
.單調增區間為![]()
當![]() 時,
時, ![]() 的單調減區間為
的單調減區間為![]()
(3)當![]() 時,要證
時,要證![]() ,即證
,即證![]()
令![]() ,只需證
,只需證![]()
∵![]()
由指數函數及幕函數的性質知: ![]() 在
在![]() 上是增函數
上是增函數
∵![]() ,∴
,∴![]() 在
在![]() 內存在唯一的零點,
內存在唯一的零點,
也即![]() 在
在![]() 上有唯一零點
上有唯一零點
設![]() 的零點為
的零點為![]() ,則
,則![]() ,即
,即![]() ,
,
由![]() 的單調性知:
的單調性知:
當![]() 時,
時, ![]() ,
, ![]() 為減函數
為減函數
當![]() 時,
時, ![]() ,
, ![]() 為增函數,
為增函數,
所以當![]() 時.
時.
![]()
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】給出下列4個命題
①“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”;
”;
②若命題![]() ,則
,則![]() 為真命題;
為真命題;
③“平面向量![]() 夾角為銳角,則
夾角為銳角,則![]() ”的逆命題為真命題;
”的逆命題為真命題;
④“函數![]() 有零點”是“函數
有零點”是“函數![]() 在
在![]() 上為減函數”的充要條件.
上為減函數”的充要條件.
其中正確的命題個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等差數列![]() 中,
中, ![]() ,其前
,其前![]() 項和為
項和為![]() ,等比數列
,等比數列![]() 的各項均為正數,
的各項均為正數, ![]() ,且
,且![]() ,
, ![]() .
.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)令 ,設數列
,設數列![]() 的前
的前![]() 項和為
項和為![]() ,求
,求![]() (
(![]() )的最大值與最小值.
)的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=a﹣ ![]() ,
,
(1)若x∈[ ![]() ,+∞),①判斷函數g(x)=f(x)﹣2x的單調性并加以證明;②如果f(x)≤2x恒成立,求a的取值范圍;
,+∞),①判斷函數g(x)=f(x)﹣2x的單調性并加以證明;②如果f(x)≤2x恒成立,求a的取值范圍;
(2)若總存在m,n使得當x∈[m,n]時,恰有f(x)∈[2m,2n],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若Ai(i=1,2,3,…,n)是△AOB所在平面內的點,且 ![]()
![]() =
= ![]()
![]() ,給出下列說法:
,給出下列說法:
·(1)| ![]() |=|
|=| ![]() |=|
|=| ![]() |=…=|
|=…=| ![]() |
|
·(2)| ![]() |的最小值一定是|
|的最小值一定是| ![]() |
|
·(3)點A和點Ai一定共線
·(4)向量 ![]() 及
及 ![]() 在向量
在向量 ![]() 方向上的投影必定相等
方向上的投影必定相等
其中正確的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊半徑為2的半圓形紙片,計劃剪裁成等腰梯形ABCD的形狀,它的下底AB是⊙O的直徑,上底CD的端點在圓周上,設CD=2x,梯形ABCD的周長為y. 
(1)求出y關于x的函數f(x)的解析式;
(2)求y的最大值,并指出相應的x值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com