
| A. | $2\overrightarrow{DB}+3\overrightarrow{DC}=0$ | B. | $3\overrightarrow{DB}+2\overrightarrow{DC}=0$ | C. | $\overrightarrow{OA}-5\overrightarrow{OD}=0$ | D. | $5\overrightarrow{OA}+\overrightarrow{OD}=0$ |
分析 由已知得$\frac{1}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}+\frac{3}{5}\overrightarrow{OC}$=$\overrightarrow{0}$,則$\frac{1}{5}\overrightarrow{OA}+\overrightarrow{OD}$=$\overrightarrow{0}$,從而得到$\overrightarrow{OA}+5\overrightarrow{OD}$=$\overrightarrow{0}$,由此能求出2$\overrightarrow{DB}$+3$\overrightarrow{DC}$=$\overrightarrow{0}$.
解答 解:∵△ABC內一點O滿足$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}$=$\overrightarrow{0}$,直線AO交BC于點D,
∴$\frac{1}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}+\frac{3}{5}\overrightarrow{OC}$=$\overrightarrow{0}$,
令$\overrightarrow{OE}$=$\frac{2}{5}\overrightarrow{OB}+\frac{3}{5}\overrightarrow{OC}$,則$\frac{1}{5}\overrightarrow{OA}+\overrightarrow{OD}$=$\overrightarrow{0}$,
∴B,C,E三點共線,A,O,E三點共線,∴D,E重合.
∴$\overrightarrow{OA}+5\overrightarrow{OD}$=$\overrightarrow{0}$,∴2$\overrightarrow{DB}$+3$\overrightarrow{DC}$=2$\overrightarrow{OB}$-2$\overrightarrow{OD}$+3$\overrightarrow{OC}$-3$\overrightarrow{OD}$=-$\overrightarrow{OA}$-5$\overrightarrow{OD}$=$\overrightarrow{0}$.
故選:A.
點評 本題考查命題真假的判斷,是基礎題,解題時要認真,注意平面向量運算法則的合理運用.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | ?x0∈R,使得f(x)<0 | |
| B. | ?x∈[0,+∞),f(x)≥0 | |
| C. | ?x1,x2∈[0,+∞),使得$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$ | |
| D. | ?x1∈[0,+∞),?x2∈[0,+∞)使得f(x1)>f(x2) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{-\frac{π}{4}+kπ,\frac{π}{4}+kπ}](k∈Z)$ | B. | $[{\frac{π}{4}+kπ,\frac{3π}{4}+kπ}](k∈Z)$ | ||
| C. | $[{\frac{π}{12}+kπ,\frac{7π}{12}+kπ}](k∈Z)$ | D. | $[{-\frac{5π}{12}+kπ,\frac{π}{12}+kπ}](k∈Z)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
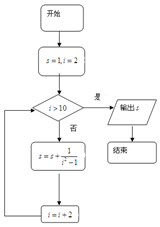
| A. | $\frac{5}{11}$ | B. | $\frac{13}{9}$ | C. | $\frac{16}{11}$ | D. | $\frac{17}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com