
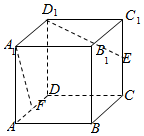
 如圖所示,在棱長為2的正方體ABCD-A1B1C1D1中,E,F分別是CC1,AD的中點,那么異面直線D1E和A1F所成角的余弦值等于$\frac{2}{5}$.
如圖所示,在棱長為2的正方體ABCD-A1B1C1D1中,E,F分別是CC1,AD的中點,那么異面直線D1E和A1F所成角的余弦值等于$\frac{2}{5}$. 分析 以D為原點建立空間直角坐標系,設正方體棱長為2.則A1(2,0,2),F)1,0,0),D1(0,0,2),E(0,2,1),則$\overrightarrow{{A}_{1}F}=(-1,0,-2)$,$\overrightarrow{{D}_{1}E}=(0,-2,-1)$,$cos<\overrightarrow{{D}_{1}E},\overrightarrow{{A}_{1}F}>$=$\frac{\overrightarrow{{D}_{1}E}•\overrightarrow{{A}_{1}F}}{|\overrightarrow{{D}_{1}E}||\overrightarrow{{A}_{1}F}|}$=$\frac{2}{\sqrt{5}×\sqrt{5}}=\frac{2}{5}$.
解答 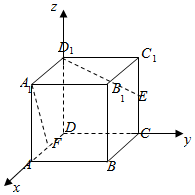 解:如圖,以D為原點建立空間直角坐標系,設正方體棱長為2.
解:如圖,以D為原點建立空間直角坐標系,設正方體棱長為2.
則A1(2,0,2),F)1,0,0),D1(0,0,2),E(0,2,1)
則$\overrightarrow{{A}_{1}F}=(-1,0,-2)$,$\overrightarrow{{D}_{1}E}=(0,-2,-1)$,
$cos<\overrightarrow{{D}_{1}E},\overrightarrow{{A}_{1}F}>$=$\frac{\overrightarrow{{D}_{1}E}•\overrightarrow{{A}_{1}F}}{|\overrightarrow{{D}_{1}E}||\overrightarrow{{A}_{1}F}|}$=$\frac{2}{\sqrt{5}×\sqrt{5}}=\frac{2}{5}$,
∴異面直線D1E和A1F所成角的余弦值等于$\frac{2}{5}$,
故答案為:$\frac{2}{5}$.
點評 本題考查了向量法求異面直線夾角,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{27}$ | B. | $\frac{2}{9}$ | C. | $\frac{2}{27}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“若x2>1,則x>1”的否命題為“若x2>1,則x≤1” | |
| B. | 命題“若α>β,則sinα>sinβ”的逆否命題為真命題 | |
| C. | 命題“?x∈R,使得x2+x+1<0”的否定是“?x∈R,都有x2+x+1>0” | |
| D. | “x2+x-2>0”的一個充分不必要條件是“x>1” |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ② | B. | ③④ | C. | ① | D. | ①④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com