
【題目】為了解某中學學生對《中華人民共和國交通安全法》的了解情況,調查部門在該校進行了一次問卷調查(共12道題),從該校學生中隨機抽取40人,統計了每人答對的題數,將統計結果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六組,得到如下頻率分布直方圖.
六組,得到如下頻率分布直方圖.
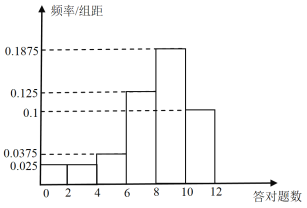
(1)若答對一題得10分,未答對不得分,估計這40人的成績的平均分(同一組中的數據用該組區間的中點值作代表);
(2)若從答對題數在![]() 內的學生中隨機抽取2人,求恰有1人答對題數在
內的學生中隨機抽取2人,求恰有1人答對題數在![]() 內的概率.
內的概率.
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() 的焦點為F,Q是拋物線上的一點,
的焦點為F,Q是拋物線上的一點,![]() .
.
(Ⅰ)求拋物線C的方程;
(Ⅱ)過點![]() 作直線l與拋物線C交于M,N兩點,在x軸上是否存在一點A,使得x軸平分
作直線l與拋物線C交于M,N兩點,在x軸上是否存在一點A,使得x軸平分![]() ?若存在,求出點A的坐標,若不存在,請說明理由.
?若存在,求出點A的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某連鎖餐廳新店開業,打算舉辦一次食品交易會,招待新老顧客試吃.項目經理通過查閱最近![]() 次食品交易會參會人數
次食品交易會參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下統計表:
(袋),得到如下統計表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數(萬人) |
|
|
|
|
|
原材料(袋) |
|
|
|
|
|
(1)根據所給![]() 組數據,求出
組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知購買原材料的費用![]() (元)與數量
(元)與數量![]() (袋)的關系為
(袋)的關系為![]() ,投入使用的每袋原材料相應的銷售收入為
,投入使用的每袋原材料相應的銷售收入為![]() 元,多余的原材料只能無償返還,據悉本次交易大會大約有
元,多余的原材料只能無償返還,據悉本次交易大會大約有![]() 萬人參加,根據(1)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤
萬人參加,根據(1)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
參考公式: ,
,![]() .
.
參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有限個元素組成的集合![]() ,
,![]() ,記集合
,記集合![]() 中的元素個數為
中的元素個數為![]() ,即
,即![]() .定義
.定義![]() ,集合
,集合![]() 中的元素個數記為
中的元素個數記為![]() ,當
,當![]() 時,稱集合
時,稱集合![]() 具有性質
具有性質![]() .
.
(1)![]() ,
,![]() ,判斷集合
,判斷集合![]() ,
,![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(2)設集合![]() ,
,![]() 且
且![]() (
(![]() ),若集合
),若集合![]() 具有性質
具有性質![]() ,求
,求![]() 的最大值;
的最大值;
(3)設集合![]() ,其中數列
,其中數列![]() 為等比數列,
為等比數列,![]() (
(![]() )且公比為有理數,判斷集合
)且公比為有理數,判斷集合![]() 是否具有性質
是否具有性質![]() 并說明理由.
并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點
為極點![]() ,軸的正半軸為極軸建立極坐標系,圓
,軸的正半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 的值;
的值;
(2)直線![]() 與圓
與圓![]() 相交于不同兩點
相交于不同兩點![]() ,
,![]() ,線段
,線段![]() 的中點為
的中點為![]() ,求點
,求點![]() 的軌跡的參數方程.
的軌跡的參數方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某校打算在長為1千米的主干道![]() 一側的一片區域內臨時搭建一個強基計劃高校咨詢和宣傳臺,該區域由直角三角形區域
一側的一片區域內臨時搭建一個強基計劃高校咨詢和宣傳臺,該區域由直角三角形區域![]() (
(![]() 為直角)和以
為直角)和以![]() 為直徑的半圓形區域組成,點
為直徑的半圓形區域組成,點![]() (異于
(異于![]() ,
,![]() )為半圓弧上一點,點
)為半圓弧上一點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() .已知
.已知![]() ,設
,設![]() ,且
,且![]() .初步設想把咨詢臺安排在線段
.初步設想把咨詢臺安排在線段![]() ,
,![]() 上,把宣傳海報懸掛在弧
上,把宣傳海報懸掛在弧![]() 和線段
和線段![]() 上.
上.
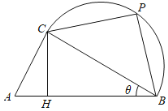
(1)若為了讓學生獲得更多的咨詢機會,讓更多的省內高校參展,打算讓![]() 最大,求該最大值;
最大,求該最大值;
(2)若為了讓學生了解更多的省外高校,貼出更多高校的海報,打算讓弧![]() 和線段
和線段![]() 的長度之和最大,求此時的
的長度之和最大,求此時的![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,要利用一半徑為![]() 的圓形紙片制作三棱錐形包裝盒.已知該紙片的圓心為
的圓形紙片制作三棱錐形包裝盒.已知該紙片的圓心為![]() ,先以
,先以![]() 為中心作邊長為
為中心作邊長為![]() (單位:
(單位:![]() )的等邊三角形
)的等邊三角形![]() ,再分別在圓
,再分別在圓![]() 上取三個點
上取三個點![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 分別是以
分別是以![]() ,
,![]() ,
,![]() 為底邊的等腰三角形.沿虛線剪開后,分別以
為底邊的等腰三角形.沿虛線剪開后,分別以![]() ,
,![]() ,
,![]() 為折痕折起
為折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合于點
重合于點![]() ,即可得到正三棱錐
,即可得到正三棱錐![]() .
.
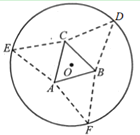

(1)若三棱錐![]() 是正四面體,求
是正四面體,求![]() 的值;
的值;
(2)求三棱錐![]() 的體積
的體積![]() 的最大值,并指出相應
的最大值,并指出相應![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知離心率為![]() 的橢圓
的橢圓![]() 的左頂點為
的左頂點為![]() ,左焦點為
,左焦點為![]() ,及點
,及點![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比數列.
成等比數列.
(1)求橢圓![]() 的方程;
的方程;
(2)斜率不為![]() 的動直線
的動直線![]() 過點
過點![]() 且與橢圓
且與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,記
兩點,記![]() ,線段
,線段![]() 上的點
上的點![]() 滿足
滿足![]() ,試求
,試求![]() (
(![]() 為坐標原點)面積的取值范圍.
為坐標原點)面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com