
【題目】對于任意的復數![]() ,定義運算
,定義運算![]() 為
為![]() .
.
(1)設集合![]() {
{![]() 均為整數},用列舉法寫出集合
均為整數},用列舉法寫出集合![]() ;
;
(2)若![]() ,
,![]() 為純虛數,求
為純虛數,求![]() 的最小值;
的最小值;
(3)問:直線![]() 上是否存在橫坐標、縱坐標都為整數的點,使該點
上是否存在橫坐標、縱坐標都為整數的點,使該點![]() 對應的復數
對應的復數![]() 經運算
經運算![]() 后,
后,![]() 對應的點也在直線
對應的點也在直線![]() 上?若存在,求出所有的點;若不存在,請說明理由.
上?若存在,求出所有的點;若不存在,請說明理由.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的右頂點
的右頂點![]() ,離心率為
,離心率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知![]() (異于點
(異于點![]() )為橢圓
)為橢圓![]() 上一個動點,過
上一個動點,過![]() 作線段
作線段![]() 的垂線
的垂線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為保護河上古橋OA,規劃建一座新橋BC,同時設立一個圓形保護區.規劃要求:新橋BC與河岸AB垂直;保護區的邊界為圓心M在線段OA上并與BC相切的圓,且古橋兩端O和A到該圓上任意一點的距離均不少于80 m.經測量,點A位于點O正北方向60 m處,點C位于點O正東方向170 m處(OC為河岸),tan∠BCO=![]() .
.

(1)求新橋BC的長;
(2)當OM多長時,圓形保護區的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點C![]() (t∈R,t≠0)為圓心的圓與x軸交于點O和點A,與y軸交于點O和點B,其中O為原點.
(t∈R,t≠0)為圓心的圓與x軸交于點O和點A,與y軸交于點O和點B,其中O為原點.
(1)求證:△OAB的面積為定值;
(2)設直線y=-2x+4與圓C交于點M,N,若OM=ON,求圓C的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,過點
,過點![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 的周長為
的周長為![]() ,
, ![]() 的離心率
的離心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)設點![]() ,
,![]() ,過點
,過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,試判斷直線
,試判斷直線![]() 與直線
與直線![]() 的交點是否恒在一條定直線上?若是,求該定直線的方程;否則,說明理由.
的交點是否恒在一條定直線上?若是,求該定直線的方程;否則,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求異面直線AB與PD所成角的余弦值;
(Ⅱ)證明:平面![]() 平面PBD;
平面PBD;
(Ⅲ)求直線DC與平面PBD所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市調研考試后,某校對甲、乙兩個文科班的數學考試成績進行分析,規定:大于或等于120分為優秀,120分以下為非優秀.統計成績后,得到如下的列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為![]() .
.
優秀 | 非優秀 | 合計 | |
甲班 | 10 | ||
乙班 | 30 | ||
合計 | 110 |
(1)請完成上面的列聯表;
(2)根據列聯表的數據,若按99.9%的可靠性要求,能否認為“成績與班級有關系”;
參考公式與臨界值表: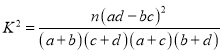 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com