
【題目】已知![]() 可以表示為一個奇函數g(x)與一個偶函數h(x)之和,若不等式
可以表示為一個奇函數g(x)與一個偶函數h(x)之和,若不等式![]() 對于
對于![]() 恒成立,則實數a的取值范圍是________.
恒成立,則實數a的取值范圍是________.
【答案】![]()
【解析】
試題依題意,g(x)+h(x)=![]() .....(1),∵g(x)是奇函數,∴g(-x)=-g(x);∵h(x)是偶函數,∴h(-x)=h(x);
.....(1),∵g(x)是奇函數,∴g(-x)=-g(x);∵h(x)是偶函數,∴h(-x)=h(x);
∴g(-x)+h(-x)="h(x)-g(x)="![]() ......(2)
......(2)
解(1)和(2)組成的方程組得h(x)=![]() ,g(x)=
,g(x)=![]()
∴ag(x)+h(2x)=a![]() +
+![]() ,∴a·
,∴a·![]() +
+![]() ≥0在x∈[1,2]恒成立
≥0在x∈[1,2]恒成立
令t=![]() ,∴
,∴![]() =
=![]() ,當x∈[1,2]時,t∈[2,4],
,當x∈[1,2]時,t∈[2,4],
∴原不等式化為a(t-![]() )+(t2+
)+(t2+![]() )≥0在t∈[2,4]上恒成立,由不等式a(t-
)≥0在t∈[2,4]上恒成立,由不等式a(t-![]() )+(t2+
)+(t2+![]() )≥0,
)≥0,
可得a(t-![]() )≥-(t2+
)≥-(t2+![]() ),∵當t∈[2,4]時,t-
),∵當t∈[2,4]時,t-![]() t>0恒成立,∴a≥
t>0恒成立,∴a≥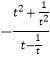 =
= =
=![]() ,即a≥
,即a≥![]() 在t∈[2,4]上恒成立,
在t∈[2,4]上恒成立,
令u=t-![]() ,求導得
,求導得![]() =1+
=1+![]() >0恒成立,∴u=t-
>0恒成立,∴u=t-![]() 在t∈[2,4]上單調遞增
在t∈[2,4]上單調遞增
∴u∈[![]() ],令f(u)=u+
],令f(u)=u+![]() ,u∈[
,u∈[![]() ],
],
求導得![]() (u)=1-
(u)=1-![]() >0在u∈[
>0在u∈[![]() ]上恒成立,∴f(u)在u∈[
]上恒成立,∴f(u)在u∈[![]() ]上單調遞增
]上單調遞增
即當u=![]() ,f(u)取最小值f(
,f(u)取最小值f(![]() )=
)=![]() ,
,
當u=![]() 時,可解得t=2(另一根不在t∈[2,4]內故舍去)
時,可解得t=2(另一根不在t∈[2,4]內故舍去)
∴當t=2時,![]() 取最小值為
取最小值為![]() ,即
,即![]() 取最大值為-
取最大值為-![]() ,∴a≥-
,∴a≥-![]() ,當t=2,x=1時取等號,∴a的最小值為-
,當t=2,x=1時取等號,∴a的最小值為-![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在空間直角坐標系![]() 中,已知正四棱錐
中,已知正四棱錐![]() 的高
的高![]() ,點
,點![]() 和
和![]() 分別在
分別在![]() 軸和
軸和![]() 軸上,且
軸上,且![]() ,點
,點![]() 是棱
是棱![]() 的中點.
的中點.
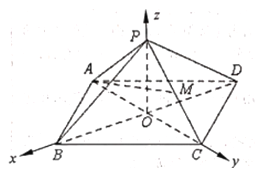
(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是( )
A.對具有線性相關關系的變量![]() 有一組觀測數據
有一組觀測數據![]() ,其線性回歸方程是
,其線性回歸方程是![]() ,且
,且![]() ,則實數
,則實數![]() 的值是
的值是![]()
B.正態分布![]() 在區間
在區間![]() 和
和![]() 上取值的概率相等
上取值的概率相等
C.若兩個隨機變量的線性相關性越強,則相關系數![]() 的值越接近于1
的值越接近于1
D.若一組數據![]() 的平均數是2,則這組數據的眾數和中位數都是2
的平均數是2,則這組數據的眾數和中位數都是2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為 為參數
為參數![]() ,以坐標原點為極點,x軸的正半軸為極軸建建立極坐標系,曲線C的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸建建立極坐標系,曲線C的極坐標方程為![]() .
.
![]() 求曲線C的直角坐標方程與直線l的極坐標方程;
求曲線C的直角坐標方程與直線l的極坐標方程;
![]() Ⅱ
Ⅱ![]() 若直線
若直線![]() 與曲線C交于點
與曲線C交于點![]() 不同于原點
不同于原點![]() ,與直線l交于點B,求
,與直線l交于點B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系.已知曲線
軸正半軸為極軸建立極坐標系.已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),![]() ,
,![]() 為過點
為過點![]() 的兩條直線,
的兩條直線,![]() 交
交![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 交
交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的傾斜角為
的傾斜角為![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的極坐標方程;
的極坐標方程;
(2)當![]() 時,求點
時,求點![]() 到
到![]() ,
,![]() ,
,![]() ,
,![]() 四點的距離之和的最大值.
四點的距離之和的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于任意的復數![]() ,定義運算
,定義運算![]() 為
為![]() .
.
(1)設集合![]() {
{![]() 均為整數},用列舉法寫出集合
均為整數},用列舉法寫出集合![]() ;
;
(2)若![]() ,
,![]() 為純虛數,求
為純虛數,求![]() 的最小值;
的最小值;
(3)問:直線![]() 上是否存在橫坐標、縱坐標都為整數的點,使該點
上是否存在橫坐標、縱坐標都為整數的點,使該點![]() 對應的復數
對應的復數![]() 經運算
經運算![]() 后,
后,![]() 對應的點也在直線
對應的點也在直線![]() 上?若存在,求出所有的點;若不存在,請說明理由.
上?若存在,求出所有的點;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com