【題目】為了解某班學生喜好體育運動是否與性別有關，對本班50人進行了問卷調查得到了如下的列聯表：
喜好體育運動 | 不喜好體育運動 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | 50 |
已知按喜好體育運動與否，采用分層抽樣法抽取容量為10的樣本，則抽到喜好體育運動的人數為6.
（1）請將上面的列聯表補充完整；
（2）能否在犯錯概率不超過0.01的前提下認為喜好體育運動與性別有關？說明理由.
附：
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，離心率
，且橢圓的短軸長為2.
（1）球橢圓的標準方程；
（2）已知直線
過右焦點
，且它們的斜率乘積為
，設分別與橢圓交于點
和
.
①求
的值；
②設
的中點
，
的中點為，求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 某廠一批產品的次品率為
，則任意抽取其中10件產品一定會發現一件次品
B. 擲一枚硬幣，連續出現5次正面向上，第六次出現反面向上的概率與正面向上的概率仍然都為0.5
C. 某醫院治療一種疾病的治愈率為10%，那么前9個病人都沒有治愈，第10個人就一定能治愈
D. 氣象部門預報明天下雨的概率是90%，說明明天該地區90%的地方要下雨，其余10%的地方不會下雨
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，過拋物線
（
）上一點
，作兩條直線分別交拋物線于點
，
，若
與
的斜率滿足
.
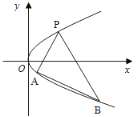
（1）證明：直線
的斜率為定值，并求出該定值；
（2）若直線在
軸上的截距
，求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為橢圓
上一點，
分別為
關于
軸，原點，
軸的對稱點，
（1）求四邊形
面積的最大值；
（2）當四邊形最大時，在線段
上任取一點
，若過的直線與橢圓相交于
兩點，且
中點恰為，求直線斜率
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題：
①若A、B、C、D是空間任意四點，則有
；
②
是
、
共線的充要條件；
③對空間任意一點P與不共線的三點A、B、C，若
，（
，y，z∈R），則P、A、B、C四點共面．
其中不正確命題的個數是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線C1的漸近線是
x±2y=0，焦點坐標是F1（-
，0）、F2（，0）．
（1）求雙曲線C1的方程；
（2）若橢圓C2與雙曲線C1有公共的焦點，且它們的離心率之和為
，點P在橢圓C2上，且|PF1|=4，求∠F1PF2的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校100名學生期中考試語文成績的頻率分布直方圖如圖所示，其中成績分組區間是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
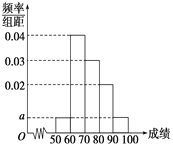
(1)求圖中a的值；
(2)根據頻率分布直方圖，估計這100名學生語文成績的平均分；
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示，求數學成績在[50,90)之外的人數.
分數段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
（
），
.
（1）若曲線
與
在它們的交點
處有相同的切線，求實數
，
的值；
（2）當
時，若函數
在區間
內恰有兩個零點，求實數a的取值范圍；
（3）當
，
時，求函數
在區間
上的最小值.
[選修4-4：坐標系與參數方程]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
