
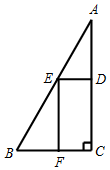
 如圖,在∠ABC=60°,∠C=90°,BC=40米的直角三角形地塊中劃出一塊矩形CDEF地塊進行綠化.
如圖,在∠ABC=60°,∠C=90°,BC=40米的直角三角形地塊中劃出一塊矩形CDEF地塊進行綠化.分析 (1)設CF=x,則BF=40-x,由矩形的面積公式建立關系式,利用矩形地塊的面積不小于$300\sqrt{3}$,求解可得AN的取值范圍;
(2)CM=m,CN=n,則有$mn=200\sqrt{3}$,利用均值不等式(注意條件,正,定,相等)可求出相應的最小值.
解答 解:(1)設CF=x,則BF=40-x.
因為∠ABC=60°,所以$EF=\sqrt{3}(40-x)$,所以${S_{CDEF}}=\sqrt{3}x(40-x)$.
由于矩形地塊的面積不小于$300\sqrt{3}$,所以有$\sqrt{3}x(40-x)≥300\sqrt{3}$,
解得CF長度的取值范圍為[10,30];
(2)由(1)可知${S_{CDEF}}=\sqrt{3}x(40-x)≤\sqrt{3}{(\frac{x+40-x}{2})^2}$$≤400\sqrt{3}$(x∈(0,40)),
當x=20時取最大值.所以矩形地塊的面積最大值為$400\sqrt{3}$.
由題意可知,當矩形的面積被分為兩塊的面積之比為1:3時,
則有${S_{CMN}}=\frac{1}{2}{S_{CDF}}$=$100\sqrt{3}$.
設CM=m,CN=n,則有$mn=200\sqrt{3}$(0<m<20,0<n<20),
所以$MN=\sqrt{{m^2}+{n^2}}$$≥\sqrt{2mn}$=$20\root{4}{3}$,當且僅當$m=n=\sqrt{200\sqrt{3}}$時取最小值.
點評 考查學生會根據實際問題選擇函數關系的能力,利用基本不等式求最值的能力,屬于中檔題.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $-\frac{3}{4}$ | C. | 0 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{12}{25}$ | B. | $\frac{24}{25}$ | C. | $\frac{12}{25}$或$-\frac{12}{25}$ | D. | $\frac{24}{25}$或-$\frac{24}{25}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2252-2 | B. | 2253-2 | C. | 21008-2 | D. | 22016-2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com