
| A. | f(x)=1,g(x)=x0 | B. | f(x)=$\root{3}{x}$,g(x)=$\frac{{x}^{2}}{x}$ | C. | f(x)=lnex,g(x)=elnx | D. | f(x)=$\frac{1}{|x|}$,g(x)=$\frac{1}{\sqrt{{x}^{2}}}$ |
分析 根據兩個函數的定義域相同,對應關系也相同,即可判斷它們是同一函數.
解答 解:對于A,f(x)=1(x∈R),與g(x)=x0=1(x≠0)的定義域不同,不是同一函數;
對于B,f(x)=$\root{3}{x}$(x∈R),與g(x)=$\frac{{x}^{2}}{x}$=x(x≠0)的定義域不同,對應關系也不同,不是同一函數;
對于C,f(x)=lnex=x(x∈R),與g(x)=elnx=x(x>0)的定義域不同,不是同一函數;
對于D,f(x)=$\frac{1}{|x|}$(x≠0),與g(x)=$\frac{1}{\sqrt{{x}^{2}}}$=$\frac{1}{|x|}$(x≠0)的定義域相同,對應關系也相同,是同一函數.
故選:D.
點評 本題考查了判斷兩個函數是否為同一函數的應用問題,是基礎題目.


科目:高中數學 來源: 題型:選擇題
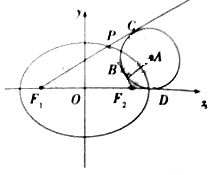 如圖,F1,F2分別是橢圓$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦點,橢圓的離心率為$\sqrt{3}$-1,P為橢圓上第一象限內的一點,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圓A與△PF1F2三邊所在直線都相切,切點分別為B,C,D,則圓A的半徑為( )
如圖,F1,F2分別是橢圓$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦點,橢圓的離心率為$\sqrt{3}$-1,P為橢圓上第一象限內的一點,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圓A與△PF1F2三邊所在直線都相切,切點分別為B,C,D,則圓A的半徑為( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$-6 | C. | 4$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0<m<3或m<-1 | B. | 0<m<3 | C. | -1<m<3 | D. | m>3或m<-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com