
| A. | 0<m<3或m<-1 | B. | 0<m<3 | C. | -1<m<3 | D. | m>3或m<-1 |
分析 先由題意求出函數為3為周期的周期函數,再根據函數為奇函數得到f(2)<2,代入解不等式即可.
解答 解:∵f($\frac{3}{2}$-x)=f(x),
∴f(x-$\frac{3}{2}$)=-f(x),
用$\frac{3}{2}$+x代換x得:f(x+$\frac{3}{2}$-$\frac{3}{2}$)=f(x)=-f(x+$\frac{3}{2}$);
用$\frac{3}{2}$+x代換x得:f(x+$\frac{3}{2}$)=-f(x+3)=-f(x);
即f(x)=f(x+3);
∴函數為以3為周期的周期函數,
∴f(x)=-f(-x),f(1)=-f(-1),f(-1)=f(2),
∴-f(2)=-f(-1)=f(1)>-2,
∴f(2)<2,
∴f(2)=m-$\frac{3}{m}$<2,
解得0<m<3,或m<-1,
故選:A
點評 本題考查函數的周期性和奇偶性的應用,解題時要認真審題,仔細解答,屬于中檔題.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=1,g(x)=x0 | B. | f(x)=$\root{3}{x}$,g(x)=$\frac{{x}^{2}}{x}$ | C. | f(x)=lnex,g(x)=elnx | D. | f(x)=$\frac{1}{|x|}$,g(x)=$\frac{1}{\sqrt{{x}^{2}}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
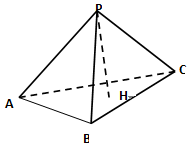 已知P為△ABC所在平面外一點,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,則H為△ABC的( )
已知P為△ABC所在平面外一點,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,則H為△ABC的( )| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 內心 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{1}{2}$,1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -5 | B. | -7 | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3+2$\sqrt{2}$ | B. | 9 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
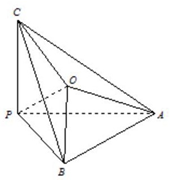 如圖,在三棱錐P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC內,∠OPC=45°,∠OPA=60°,則∠OPB的余弦值為( )
如圖,在三棱錐P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC內,∠OPC=45°,∠OPA=60°,則∠OPB的余弦值為( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com